Category: Data Representation

A visit to the Turing Machine: a short story

by Greg Michaelson

Greg Michaelson is an Emeritus professor of computer science at Heriot-Watt University in Edinburgh. He is also a novelist and a short story writer.

From the cs4fn archive.

Burning City
Image by JL G from Pixabay

“Come on!” called Alice, taking the coat off the peg. “We’re going to be late!”

“Do I have to?” said Henry, emerging from the front room.

“Yes,” said Alice, handing him the coat. “Of course you have to go. Here. Put this on.”

“But we’re playing,” said Henry, wrestling with the sleeves.

“Too bad,” said Alice, straightening the jacket and zipping it up. “It’ll still be there when we get back.”

“Not if someone knocks it over,” said Henry, picking up a small model dinosaur from the hall table. “Like last time. Why can’t we have electric games like you did?”

“Electronic games,” said Alice, doing up her buttons. “Not electric. No one has them anymore. You know that.”

“Were they really digital?” asked Henry, fiddling with the dinosaur.

“Yes,” said Alice, putting on her hat. “Of course they were digital.”

“But the telephone’s all right,” said Henry.

“Yes,” said Alice, checking her makeup in the mirror. “It’s analogue.”

“And radio. And record players. And tape recorders. And television,” said Henry.

“They’re all analogue now,” said Alice, putting the compact back into her handbag. “Anything analogue’s fine. Just not digital. Stop wasting time! We’ll be late.”

“Why does it matter if we’re late?” asked Henry, walking the dinosaur up and down the hall table.

“They’ll notice,” said Alice. “We don’t want to get another warning. Put that away. Come on.”

“Why don’t the others have to go?” asked Henry, palming the dinosaur.

“They went last Sunday,” said Alice, opening the front door. “You said you didn’t want to go. We agreed I’d take you today instead.”

“Och, granny, it’s so boring…” said Henry.

They left the house and walked briskly to the end of the street. Then they crossed the deserted park, following the central path towards the squat neo-classical stone building on the far side.

“Get a move on!” said Alice, quickening the pace. “We really are going to be late.”

————————-

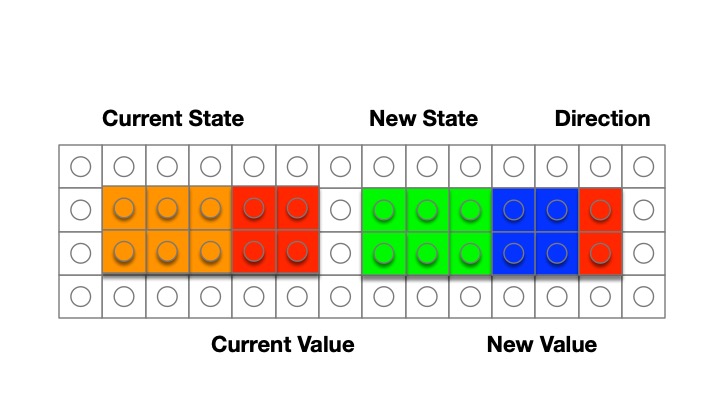
Henry really hadn’t paid enough attention at school. He knew that Turing Machines were named for Alan Turing, the first Martyr of the Digital Age. And he knew that a Turing Machine could work out sums, a bit like a school child doing arithmetic. Only instead of a pad of paper and a pencil, a Turing Machine used a tape of cells. And instead of rows of numbers and pluses and minuses on a page, a Turing Machine could only put one letter on each cell, though it could change a letter without having to actually rub it out. And instead of moving between different places on a piece of paper whenever it wanted to, and maybe doodling in between the sums, a Turing Machine could only move the tape left and right one cell at a time. But just like a school child getting another pad from the teacher when they ran out of paper, the Turing Machine could somehow add another empty cell whenever it got to the end of the tape.

————————-

When they reached the building, they mounted the stone staircase and entered the antechamber through the central pillars. Just inside the doorway, Alice gave their identity cards to the uniformed guard.

“I see you’re a regular,” she said approvingly to Alice, checking the ledger. “But you’re not,” sternly to Henry.

Henry stared at his shoes.

“Don’t leave it so long, next time,” said the guard, handing the cards back to Alice. “In you go. They’re about to start. Try not to make too much noise.”

Hand in hand, Alice and Henry walked down the broad corridor towards the central shrine. On either side, glass cases housed electronic equipment. Computers. Printers. Scanners. Mobile phones. Games consoles. Laptops. Flat screen displays.

The corridor walls were lined with black and white photographs. Each picture showed a scene of destitution from the Digital Age.

Shirt sleeved stock brokers slumped in front of screens of plunging share prices. Homeless home owners queued outside a state bank soup kitchen. Sunken eyed organic farmers huddled beside mounds of rotting vegetables. Bulldozers shovelled data farms into land fill. Lines of well armed police faced poorly armed protestors. Bodies in bags lay piled along the walls of the crematorium. Children scavenged for toner cartridges amongst shattered office blocks.

Alice looked straight ahead: the photographs bore terrible memories. Henry dawdled, gazing longingly into the display cases: Gameboy. Playstation. X Box…

“Come on!” said Alice, sotto voce, tugging Henry away from the displays.

At the end of the corridor, they let themselves into the shrine. The hall was full. The hall was quiet.

————————-

Henry was actually quite good at sums, and he knew he could do them because he had rules in his head for adding and subtracting, because he’d learnt his tables. The Turing Machine didn’t have a head at all, but it did have rules which told it what to do next. Groups of rules that did similar things were called states, so all the rules for adding were kept separately from all the rules for subtracting. Every step of a Turing machine sum involved finding a rule in the state it was working on to match the letter on the tape cell it was currently looking at. That rule would tell the Machine how to change the symbol on the tape, which way to move the tape, and maybe to change state to a different set of rules.

————————-

On the dais, lowered the Turing Machine, huge coils of tape links disappearing into the dark wells on either side, the vast frame of the state transition engine filling the rear wall. In front of the Turing Machine, the Minister of State stood at the podium.

“Come in! Come in!” he beamed at Alice and Henry. “There’s lots of space at the front. Don’t be shy.”

Red faced, Alice hurried Henry down the aisle. At the very front of the congregation, they sat down cross legged on the floor beneath the podium.

“My friends,” began the Minister of State. “Welcome. Welcome indeed! Today is a special day. Today, the Machine will change state. But first, let us be silent together. Please rise.”

The Minister of State bowed his head as the congregation shuffled to its feet.

———————–

According to Henry’s teacher, there was a different Turing Machine for every possible sum in the world. The hard bit was working out the rules. That was called programming, but, since the end of the Digital Age, programming was against the law. Unless you were a Minister of State.

————————

“Dear friends,” intoned the Minister of State, after a suitable pause. “We have lived through terrible times. Times when Turing’s vision of equality between human and machine intelligences was perverted by base greed. Times when humans sought to bend intelligent machines to their selfish wills for personal gain. Times when, instead of making useful things that would benefit everybody, humans invented and sold more and more rarefied abstractions from things: shares, bonds, equities, futures, derivatives, options…”

————————

The Turing Machine on the dais was made from wood and brass. It was extremely plain, though highly polished. The tape was like a giant bicycle chain, with holes in the centre of each link. The Machine could plug a peg into a hole to represent a one or pull a peg out to represent a zero. Henry knew that any information could be represented by zeros and ones, but it took an awful lot of them compared with letters.

————————-

“… Soon there were more abstractions than things, and all the wealth embodied in the few things that the people in poor countries still made was stolen away, to feed the abstractions made by the people in the rich countries. None of this would have been possible without computers…”

————————-

The state transition unit that held the rules was extremely complicated. Each rule was a pattern of pegs, laid out in rows on a great big board. A row of spring mounted wooden fingers moved up and down the pegs. When they felt the rule for the symbol on the tape cell link, they could trigger the movement of a peg in or out of the link, and then release the brakes to start up one revolution of the enormous cog wheels that would shift the tape one cell left or right.

A stone looking like a scared face
Image by Dean Moriarty from Pixabay

————————-

“…With all the computers in the world linked together by the Internet, humans no longer had to think about how to manage things, about how best to use them for the greatest good. Instead, programs that nobody understood anymore made lightening decisions, moving abstractions from low profits to high profits, turning the low profits into losses on the way, never caring how many human lives were ruined…”

————————-

The Turing Machine was powered by a big brass and wooden handle connected to a gear train. The handle needed lots of turns to find and apply the next rule. At the end of the ceremony, the Minister of State would always invite a member of the congregation to come and help him turn the handle. Henry always hoped he’d be chosen.

——————————

“…Turing himself thought that computers would be a force for untold good; that, guided by reason, computers could accomplish anything humans could accomplish. But before his vision could be fully realised, he was persecuted and poisoned by a callous state interested only in secrets and profits. After his death, the computer he helped design was called the Pilot Ace; just as the pilot guides the ship, so the Pilot Ace might have been the best guide for a true Digital Age…”

——————————

Nobody was very sure where all the cells were stored when the Machine wasn’t inspecting them. Nobody was very sure how new cells were added to the ends of the tape. It all happened deep under the dais. Some people actually thought that the tape was infinite, but Henry knew that wasn’t possible as there wasn’t enough wood and brass to make it that long.

——————————

“…But almost sixty years after Turing’s needless death, his beloved universal machines had bankrupted the nations of the world one by one, reducing their peoples to a lowest common denominator of abject misery. Of course, the few people that benefited from the trade in abstractions tried to make sure that they weren’t affected but eventually even they succumbed…”

——————————

Nobody seemed to know what the Turing Machine on the dais was actually computing. Well, the Minister of State must have known. And Turing had never expected anyone to actually build a real Turing Machine with real moving parts. Turing’s machine was a thought experiment for exploring what could and couldn’t be done by following rules to process sequences of symbols.

——————————

“…For a while, everything stopped. There were power shortages. There were food shortages. There were medical shortages. People rioted. Cities burned. Panicking defence forces used lethal force to suppress the very people they were supposed to protect. And then, slowly, people remembered that it was possible to live without abstractions, by each making things that other people wanted, by making best use of available resources for the common good…”

——————————

The Turing Machine on the dais was itself a symbol of human folly, an object lesson in futility, a salutary reminder that embodying something in symbols didn’t make it real.

——————————

“…My friends, let us not forget the dreadful events we have witnessed. Let us not forget all the good people who have perished so needlessly. Let us not forget the abject folly of abstraction. Let the Turing Machine move one step closer along the path of its unknown computation. Let the Machine change its state, just as we have had to change ours. Please rise.”

The congregation got to their feet and looked expectantly at the Minister of State. The Minister of State slowly inspected the congregation. Finally, his eyes fixed on Henry, fidgeting directly in front of him.

“Young man,” he beamed at Henry. “Come. Join me at the handle. Together we shall show that Machine that we are all its masters.”

Henry looked round at his grandmother.

“Go on,” she mouthed. “Go on.”

Henry walked round to the right end of the dais. As he mounted the wooden stairs, he noticed a second staircase leading down behind the Machine into the bowels of the dais.

“Just here,” said the Minister of State, leading Henry round behind the handle, so they were both facing the congregation. “Take a good grip…”

Henry was still clasping the plastic dinosaur in his right hand. He put the dinosaur on the nearest link of the chain and placed both hands on the worn wooden shaft.

And turn it steadily…”

Henry leant into the handle, which, much to his surprise, moved freely, sweeping the wooden fingers across the pegs of rules on the state transition panel. As the fingers settled on a row of pegs, a brass prod descended from directly above the chain, forcing the wooden peg out of its retaining hole in the central link. Finally, the chain slowly began to shift from left to right, across the front of the Machine, towards Henry and the Minister of State. As the chain moved, the plastic dinosaur toppled over and tumbled down the tape well.

“Oh no!” cried Henry, letting go of the handle. Utterly nonplussed, the Minister of State stood and stared as Henry peered into the shaft, rushed to the back of the Machine and hurried down the stairs into the gloom.

A faint blue glow came from the far side of the space under the dais. Henry cautiously approached the glow, which seemed to come from a small rectangular source, partly obscured by someone in front of it.

“Please,” said Henry. “Have you seen my dinosaur?”

“Hang on!” said a female voice.

The woman stood up and lit a candle. Looking round, Henry could now see that the space was festooned with wires, leading into electric motors driving belts connected to the Turing Machine. The space was implausibly small. There was no room for a finite tape of any length at all, let alone an infinite one.

“Where are all the tape cells?” asked Henry, puzzled.

“We only need two spare ones,” said the woman. “When the tape moves, we stick a new cell on one end and take the cell off the other.”

“So what’s the blue light?” asked Henry.

“That’s a computer,” said the woman. “It keeps track of what’s on the tape and controls the Turing Machine.”

“A real digital computer!” said Henry in wonder. “Does it play games?”

“Oh yes!” said the woman, turning off the monitor as the Minister of State came down the stairs. “What do you think I was doing when you showed up? But don’t tell anyone. Now, let’s find that dinosaur.”

Related Magazines …

cs4fn issue 14 cover

More on …

EPSRC supports this blog through research grant EP/W033615/1,

Lego Computer Science: Turing Machines Part 3: the program

by Paul Curzon, Queen Mary University of London

We have so far built the hardware of a Lego Turing Machine. Next we need the crucial part: software. It needs a program to tell it what to do.

Our Turing Machine so far has an Infinite Tape, a Tape Head and a Controller. The Tape holds data values taken from a given set of 4×4 bricks. It starts in a specific initial pattern: the Initial Tape. There is also a controller. It holds different coloured 3×2 bricks representing an initial state, an end state, a current state and has a set of other possible states (so coloured bricks) to substitute for the current state.

Why do we need a program?

As the machine runs it changes from one state to another, and inputs from or outputs to the tape. How it does that is governed by its Program. What is the new state, the new value and how does the tape head move? The program gives the answers. The program is just a set of instructions the machine must blindly follow. Each instruction is a single rule to follow. Each program is a set of such rules. In our Turing Machines, these rules are not set out in an explicit sequence as happens in a procedural program, say. It uses a different paradigm for what a program is. Instead at any time only one of the set of rules should match the current situation and that is the one that is followed next.

Individual Instructions

A single rule contains five parts: a Current State to match against, a Current Value under the Tape Head to match against, a New State to replace the existing one, and a New Value to write to the tape. Finally, it holds a Direction to Move the Tape Head (left or right or stay in the same place). An example might be:

  • Current State: ORANGE
  • Current Value: RED
  • New State: GREEN
  • New Value: BLUE
  • Direction: RIGHT

But what does a rule like this actually do?

What does it mean?

You can think of each instruction as an IF-THEN rule. The above rule would mean:

IF 

  •    the machine is currently in state ORANGE AND    
  •    the Tape Head points to RED 

THEN (take the following actions)

  •     change the state to GREEN, 
  •     write the new value BLUE on the tape AND THEN
  •     move the tape head RIGHT.

This is what a computer scientist would call the programming language Semantics. The semantics tell you what program instructions mean, so what they do.

Representing Instructions in Lego

We will use  a series of 5 bricks in a particular order to represent the parts of the rule. For example, we will use a yellow 3×2 brick in the first position of a rule to represent the fact that the rule will only trigger if the current state is yellow. A blue 2×2 brick in the second position will mean the rule will also only trigger if the current value under the tape head is blue. We will use a grey brick to mean an empty tape value. The third and fourth position will represent the new state and new value if the rule does trigger. To represent the direction to move we will use a 1×2 Red brick to mean move Right, and a 1×2 yeLLow brick to mean move Left. We will use a black 1×2 brick to mean do not move the tape head (mirroring the way we are also using black to mean do nothing in the sense of the special end state). The above rule would therefore be represented in Lego as below. 

A Turing machine instruction Current state: orange Currnent value red New state green New value blue Direction red
A single instruction for a Lego Turing Machine

Notice we are using the same colour to represent different things here. The representation is the colour combined with the size of brick and position in the rule. So a Red brick can mean a red state (a red 3×2 brick) or a red value (a red 2×2 brick) or move right (a red 1×2 brick).

Lego programs

That is what a rule, so single Turing Machine instruction, looks like. Programs are just a collection of such rules: so a series of lines of bricks.

Suppose we have a Turing machine with two states (Red and Orange) and two values on the tape (Blue or Empty), then a complete program would have 4 rules, one for each possible combination. We have given one example program below. If there were more states or more possible data values then the program would be correspondingly bigger to cover all the possibilities.

A Turing Machine Program Red-Blue -> Red-Blue-Red Red-Grey -> Orange-Blue-Yellow Orange-Blue -> Orange-Blue-Yellow Orange-Grey -> Black-Grey-Red
A 4 instruction Turing Machine Program for a Turing Machine with two states (Red, Orange) and two data values (Blue, Empty)

A Specific Turing Machine

Exactly what it does will depend on its input – the initial tape it is given to process, as well as the initial state and where the tape head initially points to. Perhaps you can work out what the above program does given a tape with an empty value followed by a series of three blue bricks (and then empty data values off to infinity (the blank value is the only value that is allowed to appear an infinite number of times on an initial tape) and the Head pointing to the rightmost blue brick value. The initial state is red. See the Lego version of this specific machine below.

A Turing Machine with Tape, Controller and Program.
A full Turing Machine ready to execute.

Note something we have glossed over. You also potentially need an infinite number of bricks of each value that is allowed on the tape. We have a small pile, but you may need that Lego factory we mentioned previously, so that as the Turing Machine runs you always have a piece to swap on to the machine tape when needed. Luckily, for this machine a small number of bricks should be enough (as long as you do not keep running it)!

What does this Turing Machine do? We will look at what it does and how to work it out in a future article. In the meantime try and work out what it does with this tape, but also what it does if the tape has more or less blue bricks in a row on it to start with (with everything else kept the same).

Note that, to keep programs smaller, you could have a convention that if no rule fits a situation then it means the program ends. Then you could have fewer rules in some programs. However,  that would just be shorthand for there being extra rules with black new states, the tape being left alone, and the tape head moves right. In real programming, it is generally a good idea to ALWAYS be explicit about what you intend the program to do, as otherwise it is an easy way for bugs to creep in, for example, because you just forgot to say in some case.

Alan Turing invented Turing Machines before any computer existed. At the time a “computer” was a person who followed rules to do calculations (just like you were taught the rules to follow to do long multiplication at primary school, for example). His idea was therefore that a human would follow the rules in a Turing Machine program, checking the current state and value under the tape head, and changing the state, the value on the tape and the movement of the head. A person provides the power and equivalent of a robotic arm that follows the underlying Turing Machine algorithm: the Turing Machine algorithm that if followed causes each Turing Machine’s program to execute.

If a human animating the machine was good enough for Turing, it is good enough for us, so that is how our Lego Turing Machines will work. Your job will be to follow the rules and so operate the machine. Perhaps, that is exactly what you did to work out what the program above does!

Next we will look at how to work out what a Turing Machine does. Then it will be time to write, then run, some Turing Machine programs of your own…

More Lego Computer Science

Image shows a Lego minifigure character wearing an overall and hard hat looking at a circuit board, representing Lego Computing
Image by Michael Schwarzenberger from Pixabay

Part of a series featuring featuring pixel puzzles,
compression algorithms, number representation,
gray code, binary and computation.

Related Magazines …

cs4fn issue 14 cover

More on …

EPSRC supports this blog through research grant EP/W033615/1, The Lego Computer Science post was originally funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.

Lego Computer Science: Turing Machines Part 2: the controller

by Paul Curzon, Queen Mary University of London

Last time we started to build a working computer out of Lego: a Turing Machine. So far we have seen that we can make the memory of a Turing Machine (its Infinite Tape) in Lego. We can also create a movable Tape Head that marks the position where data can be read from and written to the tape (see image).

Controlling states

How does the machine decide where and when to move the Tape Head, though? It has a Controller. The key part of the controller is that it holds a Current State of the machine. Think of traffic lights for what we mean by the state of a machine. In the UK traditional traffic lights have a Red state, an Amber state, a Green state and a Red-Amber state. Each means a different thing (such as “Stop” and “Go”). The controller of the lights moves between these different internal states. With a traffic light, the current internal state is also shown to the world by the lights that light up! Machine states do not have to be visible to the outside world, however. In fact, they only are if the person who designs the interface makes them visible. For most machines, only some of their internal state is made visible. In our Turing Machine we will be able to see the states as they will be visible in the controller. However, the output of a Turing Machine is the state of the tape, so if we wanted the states to really be visible we would write a version on to the tape. You can then imagine the tape triggering external lights to come on or off, or change colour as a simple form of actual output. This is what Computer Scientists call memory-mapped peripherals – where to send data (output) to a peripheral device (a screen, a panel of lights, a printer, or whatever, you write to particular locations in memory, and that data is read from there by the peripheral device. That is going beyond the pure idea of a Turing Machine though, where the final state of the machine when it stops is its output.

Representing States

How do we represent states in Lego? Any finite set of things (symbols) could be used to represent the different states (including numbers or binary codes, for example). We will use different coloured 3×2 blocks. Each colour of block will stand for a different state that the machine is in. The controller will have a space that holds the brick representing the Current State. It will also have space for a set of places for the blocks representing the other allowable states of this Turing Machine. As the machine runs, the state will change as represented by swapping one of these state bricks for another.

Different Turing Machines can allow a different number of possible states the machine could be in, so this part of the controller might be bigger or smaller depending on the machine and what it needs to do its job. Again think of traffic lights, in some countries, and on pedestrian crossings there are only two states, a Red state (stop) and a Green state (go). Its controller only needs two states so we would only need two different coloured bricks.

A Turing Machine Controller with current state red, end state black and three other possible states (green, orange and blue)

Initial States

The current state will always start in some initial state when the machine first starts up. It is useful to record in the controller what state that is so that each time we restart the machine anew it can be reset. We will just put a block in the position next to the current state to indicate what the initial state should be. We won’t ever change it for a given machine.

End States

One of the states of a Turing Machine is always a special End State. We will always use a black brick to represent this. Whatever is used has to be specified at the outset, though. When not in use we will keep the end state brick next to the initial state brick. Once the machine finishes operations it will enter this End State, or put another way, if the black brick ever becomes the current state brick the machine will stop. From that point on the machine will do nothing. Some machines might never reach an end state, they just go on forever. Traffic lights just cycle round the states forever, for example, never reaching an end state. Other machines do end though. For example, a kettle controller stops the machine when the water has boiled. An addition Turing Machine might end when it has output the answer to an addition. To do another addition you would start it up again with new information on the tape indicating what it was to add.

We have now created the physical part of the Turing Machine. All we need now is a Program to tell it what to do! Programs come next in Part 3…

More Lego Computer Science

Image shows a Lego minifigure character wearing an overall and hard hat looking at a circuit board, representing Lego Computing
Image by Michael Schwarzenberger from Pixabay

Part of a series featuring featuring pixel puzzles,
compression algorithms, number representation,
gray code, binary and computation.

Related Magazines …

cs4fn issue 14 cover

More on …

EPSRC supports this blog through research grant EP/W033615/1, The Lego Computer Science post was originally funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.

Lego Computer Science: Turing Machines Part 1: the tape

by Paul Curzon, Queen Mary University of London

It it possible to make a working computer out of lego and you do not even have to pay for an expensive robot Mindstorm kit…but only if you are willing to provide the power yourself.

A machine in theory

In fact, Alan Turing, grandfather of Computer Science worked out how to do it before the War and before any actual computer existed. His version also needed humans to power it. Now we call it a Turing Machine and it is a theoretical model of what is computable by any machine.

The Tape

To make a working Turing Machine you first need to build an infinitely long Tape that can hold Symbols, representing data values, along it at fixed intervals. That is easy (as long as you have a lego factory). You just need to create a long line of flat pieces, say 2 studs wide. Each 2×2 square on it is then a position on the Tape. 

An infinite tape out of Lego (relies on having a Lego factory at the right-hand end churning out new tape if and when it is needed...
An infinite tape out of Lego (relies on having a Lego factory at the right-hand end churning out new tape if and when it is needed…

Be lazy

Of course you can’t actually make it infinitely long, but you can make it longer every time you need some more of it (so no problem if you do have a lego factory to churn out extra bricks as needed!) This approach to dealing with infinite data structures where you just make it bigger only when needed is now called lazy programming by computer scientists and is an elegant way that functional programs deal with input that needs to represent an infinite amount of input…It is also the way some games (like Minecraft) represent worlds or even universes. Rather than create the whole universe at the start, things over the horizon, so out of sight, are only generated if a player ever goes there – just-in-time world generation! Perhaps our universe is like that too, with new galaxies only fleshed out as we develop the telescopes to see them!

Fill it with data

The Tape has a set of Data Symbols that can appear on it that act as the Data Values of the machine. Traditional computers have symbols 0 and 1 underpinning them, so we could use those as our symbols, but in a Turing Machine we can have any set of symbols we like: ten digits, letters, Egyptian hieroglyphs, or in fact any set of symbols we want to make up. In a lego Turing Machine we can just use different coloured blocks as our symbols. If our tape is made of grey pieces then we could use red and blue for the symbols that can appear on it. Every position on the tape will then either hold a red block or a blue block. We could also allow EMPTY to be a symbol too in which case some 2×2 slots could be empty to mean that.

A tape containing data where the allowed symbols are EMPTY, RED and BLUE
A tape containing data where the allowed symbols are EMPTY, RED and BLUE

To start with

Any specific Turing Machine has an Initial Tape. This is the particular data that is on the tape at the start, before it is switched on. As the machine runs, the tape will change.

The tape with symbols on it takes the place of our computer’s memory. Just as a modern computer stores 1s and 0s in memory, our Lego Turing Machine stores its data as symbols on this tape. 

The Head

A difference is that modern computers have “random access memory” – you can access any point in memory quickly. Our tape will be accessed by a Tape Head that points to a position on the tape and allows you to read or change the data only at the point it is at. Make a triangular tape head out of lego so that it is clear which point on the tape it is pointing at. We have a design choice here. Either the Tape moves or the Head moves. As the tape could be very long so hard to move we will move the Head along beside it, so create a track for the Head to move along parallel to the tape. It will be able to move 2 studs at a time in either direction so that each time it moves it is pointing to a new position on the tape.

An infinite tape with Head (yellow) pointing at position 4 on the tape.
An infinite tape with Head (yellow) pointing at position 4 on the tape.

We have memory

We now have the first element in place of a computer, then: Memory. The next step will be to provide a way to control the tape head and how data is written to and read from the tape and so computation actually happen. (For that you need a controller which we cover in Part 2…).

More Lego Computer Science

Image shows a Lego minifigure character wearing an overall and hard hat looking at a circuit board, representing Lego Computing
Image by Michael Schwarzenberger from Pixabay

Part of a series featuring featuring pixel puzzles,
compression algorithms, number representation,
gray code, binary and computation.

Related Magazines …

cs4fn issue 14 cover

More on …

EPSRC supports this blog through research grant EP/W033615/1, The Lego Computer Science post was originally funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.

Eggheads: helping us to visualise objects and classes

by Daniel Gill, Queen Mary University of London

Past CS4FN articles have explored object-oriented programming through self-aware pizza and Strictly Come Dancing judges. But, if you’re one of those people who like to learn visually, it can be challenging to imagine what an object or class looks like. This article will hopefully help you to both think more about what makes this paradigm so useful as well as to give you a way to visualise objects.

Ada the Egghead
by Daniel Gill

To begin this adventure, I’d like to introduce Ada. Ada is an example of the newly discovered species egghead. Every egghead has very distinctive hair and eye colours. For example, Ada’s hair is a delightfully bright pink, and their eyes, a deep red. Despite their appearance, the egghead has a vicious roar intended to ward off predators, or indeed poachers.

Classes

As computer scientists, we might want to represent different eggheads in a program, but we don’t really want to store information about the eggheads with a written description or an image, because this would be harder than need-be for a computer to ‘understand’ (or rather to process as they don’t understand as such). Instead, we can store lots of individual features together, so that the computer can find out exactly what it needs from each egghead.

Egghead class

One way to achieve this is by using a class. A class is a template which contains spaces for us to fill in details for the thing we want to represent. For the egghead, we might want to store data about their name, hair colour, and eye colour – then we can fill in the template for each of the eggheads we find. These individual features are often called attributes. In a program, these attributes would be represented with variables: a place where a value, a piece of data, is stored. We can visualise a class therefore as a box with gaps to fill in for the attributes like the one on the left.

From this image, you will see alongside the attributes, we also have an image of a button for roaring. As well as storing attributes, we also define behaviours. These are actions that we can perform on the thing being represented. We visualise any behaviour as such a button. For this example, we could imagine that pressing this button might provoke the egghead causing them to roar. In programming, a behaviour is represented by a procedure, some pre-defined code that when executed makes something happen. A button that causes something to happen is a simple way to visualise such procedures.

A key point to realise is that this class is simply a template – it isn’t storing any information, nor will the roar button work. We have no actual eggheads yet… That is where objects come in.

Objects

You may have noticed that I have been using the word thing to represent the actual thing (here eggheads) that we are representing with the class. This is to avoid using the word object, which has its own special meaning, in, you guessed it, object-oriented programming. If we want to actually use our class, we need to make an instance. That just means filling in the relevant details about the specific egghead we want to store. This instance is called an object.

Let’s imagine we want to store a representation of Ada in our program. We would take an instance of the Egghead class and fill in their details. The resulting object would represent Ada, whereas the class we started with represents all and any egghead that might ever exist. Below, you can see the objects for Ada and some of Ada’s friends; Alan and Edsger. We still visualise objects as boxes, just like classes, except now the gaps are all filled in.

Objects representing Ada, Alan and Edsger

We (or a computer) could even take the given features of Alan and Edsger and generate an image of what they might look like. We have everything we need here to create something that looks and behaves like an egghead. This method of storing data means that a program can take whatever information it might want directly from the object. Likewise, it can do the equivalent of pressing the roar button and make each individual egghead roar.

Hiding the Details

Trying to change Alan’s eye colour

One thing we should consider while making the class is the integrity of the data. In its current form, any other part of our program, or another program using our class, can directly edit the attributes stored. Another part of the program (perhaps representing a virtual world for a virtual egghead to live in) might accidentally change the eye colour attribute for Alan, for example. This wouldn’t change Alan’s actual eye colour (which couldn’t happen anyway!), so our data would then be wrong. We can’t have that!

We can fix this by hiding the eye colour from the rest of the program, so it is stored within the object, but not accessible outside of it. But we still need a way for the program to read it: for this we use a button in our picture of the Egghead class. The existence of the eye colour attribute can then only be seen by other parts of the program by a procedure that gets the eye colour. No similar procedure is given for changing the eye colour, so there is no way to do it by mistake. Let’s build this new version of our class.

(a) Our new class, (b) An object representing Edsger, with eye colour hidden, (c) Pressing GetEyes gives us the eye colour.

This concept of hiding details is sometimes called encapsulation or information hiding, but computer scientists disagree about what these terms refer to exactly. Encapsulation is broader in its meanings, whereas information hiding is closer to what we are trying to do here. This video by ArjanCodes (see below) explains this distinction further.

We could change our class to include this concept for the name and hair colour, too. Whilst it is entirely possible for these attributes to change, it turns out that it is a good idea to hide them too: so hide name and use SetName and GetName buttons. That allows us to control the type of data we have going into that attribute (for example, checking the given name isn’t a number, which as all egghead names are made of letters would be a mistake).

Where next?

Now we have a class that represents all eggheads, we can store the details of any new egghead efficiently and safely. Hold on… some last-minute breaking news: scientists have found a new sub-species of egghead they are calling a rainbow egghead. All rainbow eggheads have rainbow hair, and a unique roar. Next time, we’ll use the concept of inheritance to give a more efficient way to write programs that store information about eggheads.

Image credits: all images were created by the author, Daniel Gill.

EPSRC supports this blog through research grant EP/W033615/1.

Equality, diversity and inclusion in the R Project: collaborative community coding & curating with Dr Heather Turner

You might not think of a programming language like Python or Scratch as being an ‘ecosystem’ but each language has its own community of people who create and improve its code, flush out the bugs, introduce new features, document any changes and write the ‘how to’ guides for new users. 

The logo for the R project.

R is one such programming language. It’s named after its two co-inventors (Ross Ihaka and Robert Gentleman) and is used by around two million people around the world. People working in all sorts of jobs and industries (for example finance, academic research, government, data journalists) use R to analyse their data. The software has useful tools to help people see patterns in their data and to make sense of that information. 

It’s also open source which means that anyone can use it and help to improve it, a bit like Wikipedia where anyone can edit an article or write a new one. That’s generally a good thing because it means everyone can contribute but it can also bring problems. Imagine writing an essay about an event at your school and sharing it with your class. Then imagine your classmates adding paragraphs of their own about the event, or even about different events. Your essay could soon become rather messy and you’d need to re-order things, take bits out and make sure people hadn’t repeated something that someone had already said (but in a slightly different way). 

When changes are made to software people also want to keep a note not just of the ‘words’ added (the code) but also to make a note of who added what and when. Keeping good records, also known as documentation, helps keep things tidy and gives the community confidence that the software is being properly looked after.

Code and documentation can easily become a bit chaotic when created by different people in the community so there needs to be a core group of people keeping things in order. Fortunately there is – the ‘R Core Team’, but these days its membership doesn’t really reflect the community of R users around the world. R was first used in universities, particularly by more privileged statistics professors from European countries and North America (the Global North), and so R’s development tended to be more in line with their academic interests. R needs input and ideas from a more diverse group of active developers and decision-makers, in academia and beyond to ensure that the voices of minoritised groups are included. Also the voices of younger people, particularly as many of the current core group are approaching retirement age.

Dr Heather Turner from the University of Warwick is helping to increase the diversity of those who develop and maintain the R programming language and she’s been given funding by the EPSRC* to work on this. Her project is a nice example of someone who is bringing together two different areas in her work. She is mixing software development (tech skills) with community management (people skills) to support a range of colleagues who use R and might want to contribute to developing it in future, but perhaps don’t feel confident to do so yet. 

Development can involve things like fixing bugs, helping to improve the behaviour or efficiency of programs or translating error messages that currently appear on-screen in the English language into different languages. Heather and her colleagues are working with the R community to create a more welcoming environment for ‘newbies’ that encourages participation, particularly from people who are in the community but who are not currently represented or under-represented by the core group and she’s working collaboratively with other community organisations such as R-Ladies, LatinR and RainbowR. Another task she’s involved in is producing an easier-to-follow ‘How to develop R’ guide.

There are also people who work in universities but who aren’t academics (they don’t teach or do research but do other important jobs that help keep things running well) and some of them use R too and can contribute to its development. However their contributions have been less likely to get the proper recognition or career rewards compared with those made by academics, which is a little unfair. That’s largely because of the way the academic system is set up. 

Generally it’s academics who apply for funding to do new research, they do the research and then publish papers in academic journals on the research that they’ve done and these publications are evidence of their work. But the important work that supporting staff do in maintaining the software isn’t classified as new research so doesn’t generally make it into the journals, so their contribution can get left out. They also don’t necessarily get the same career support or mentoring for their development work. This can make people feel a bit sidelined or discouraged. 

Logo for the Society of Research Software Engineering

To try and fix this and to make things fairer the Society of Research Software Engineering was created to champion a new type of job in computing – the Research Software Engineer (RSE). These are people whose job is to develop and maintain (engineer) the software that is used by academic researchers (sometimes in R, sometimes in other languages). The society wants to raise awareness of the role and to build a community around it. You can find out what’s needed to become an RSE below. 

Heather is in a great position to help here too, as she has a foot in each camp – she’s both an Academic and a Research Software Engineer. She’s helping to establish RSEs as an important role in universities while also expanding the diversity of people involved in developing R further, for its long-term sustainability.

Further reading

*Find out more about Heather’s EPSRC-funded Fellowship: “Sustainability and EDI (Equality, Diversity, and Inclusion) in the R Project” https://gtr.ukri.org/projects?ref=EP%2FV052128%2F1 and https://society-rse.org/getting-to-know-your-2021-rse-fellows-heather-turner/ 

Find out more about the job of the Research Software Engineer and the Society of Research Software Engineering https://society-rse.org/about/ 

Example job packs / adverts

Below are some examples of RSE jobs (these vacancies have now closed but you can read about what they were looking for and see if it might interest you in the future).

Note that these documents are written for quite a technical audience – the people who’d apply for the jobs will have studied computer science for many years and will be familiar with how computing skills can be applied to different subjects.

1. The Science and Technology Facilities Council (STFC) wanted four Research Software Engineers (who’d be working either in Warrington or Oxford) on a chemistry-related project (‘computational chemistry’ – “a branch of chemistry that uses computer simulation to assist in solving chemical problems”) 

2. The University of Cambridge was looking for a Research Software Engineer to work in the area of climate science – “Computational modelling is at the core of climate science, where complex models of earth systems are a routine part of the scientific process, but this comes with challenges…”

3. University College London (UCL) wanted a Research Software Engineer to work in the area of neuroscience (studying how the brain works, in this case by analysing the data from scientists using advanced microscopy).

EPSRC supports this blog through research grant EP/W033615/1.

CS4FN Advent 2023 – Day 1: Woolly jumpers, knitting and coding

Welcome to the first ‘window’ of the CS4FN Christmas Computing Advent Calendar. The picture on the ‘box’ was a woolly jumper with a message in binary, three letters on the jumper itself and another letter split across the arms. Can you work out what it says? (Answer at the end).

Come back tomorrow for the next instalment in our Advent series.

Cartoon of a green woolly Christmas jumper with some knitted stars and a message “knitted” in binary (zeroes and ones). Also the symbol for wifi on the cuffs.

Wrap up warmly with our first festive CS4FN article, from Karen Shoop, which is all about the links between knitting patterns and computer code. Find out about regular expressions in her article: Knitters and Coders: separated at birth?

Knitters and Coders: separated at birth?
Click to read Karen’s article

Image credit: Regular Expressions by xkcd

Further reading

Dickens Knitting in Code – this CS4FN article, by Paul Curzon, is about Charles Dickens’ book A Tale of Two Cities. One of the characters, Madame Defarge, takes coding to the next level by encoding hidden information into her knitting, something known as steganography (basically hiding information in plain sight). We have some more information on the history of steganography and how it is used in computing in this CS4FN article: Hiding in Elizabethan binary.

In Craft, Culture, and Code Shuchi Grover also considers the links between coding and knitting, writing that “few non-programming activities have such a close parallels to coding as knitting/crocheting” (see section 4 in particular, which talks about syntax, decomposition, subroutines, debugging and algorithms).

Something to print and colour in

This is a Christmas-themed thing you might enjoy eating, if you’ve any room left of course. Puzzle solution tomorrow. This was designed by Elaine Huen.

Solving the Christmas jumper code

The jumper’s binary reads

01011000

01001101

01000001

01010011

What four letters might be being spelled out here? Each binary number represents one letter and you can find out what each letter is by looking at this binary-to-letters translator. Have a go at working out the word using the translator (but the answer is at the end of this post).

Keep scrolling

Bit more

The Christmas jumper says… XMAS

Advert for our Advent calendar
Click the tree to visit our CS4FN Christmas Computing Advent Calendar

EPSRC supports this blog through research grant EP/W033615/1.

Why the Romans were pants at maths

Paul Curzon, Queen Mary University of London

The Romans were great at counting and addition but they were absolutely pants at multiplication. It wasn’t because they were stupid. It was because they hadn’t invented a good way to represent numbers, and that meant they needed really convoluted algorithms.

The Roman system is based on an earlier really simple way of writing numbers. You just put a line for each thing you’ve counted. Its probably the way shepherds kept count of sheep, drawing a line for each sheep. Those lines turned into the Roman letter I. To add 1 to a number you just add another I. You count: I, II, III, and so on and it makes counting easy.

Roman number blocks image by Clker-Free-Vector-Images from Pixabay

This system is called unary – whereas binary involves counting with two symbols, 1 and 0, in unary you only have one symbol to count with. Addition in unary is easy too at least for small numbers. Take the first number and add on the end all the Is for the second and you’ve got the answer number. This is exactly the way we all start doing addition on our fingers.To add 2+3, hold up 2 fingers (II) then hold up another three fingers (III) and you have the answer (IIIII).

This is fine for small numbers but it gets a bit tedious as the numbers increase (and you run out of fingers!) Comparing numbers is easy in principle – do you have the same number of Is, but hard in practice for large numbers. We can’t keep all those Is in our head so a large number is hard to think about. To get round this the Romans invented new letters to stand for groups of Is. This is what we do when we tally numbers making a crossbar for every fifth number we count. It helps us keep track of larger numbers. The Romans invented a whole bunch of symbols to help: so for example in the Roman numeral system, V stands for 5 (IIIII), X stands for 10, L for 50, C for 100, D for 500 and M for 1000. They had invented a new way to represent numbers.

Image by Katie Rose from Pixabay

This makes it much easier to write and compare larger numbers. Now when counting and you get up to 5 you just replace all those Is with a V and then carry on adding Is: VI, VII, VIII, VIIII. Then you get to VIIIII (10) so replace it all with an X, starting again adding a new lot of Is: XI, XII, XIII, XIIII, XV, and so on. Counting large numbers is now a bit more involved – the algorithm involves more than just adding an I on the end, but it is much more convenient. The addition algorithm has now become more complicated, though it is still fairly simple too. Take any two numbers to add like VII and VIII and string them together: VIIVIII. Now group together the same letters: VVIIIII. Anywhere you have enough to replace symbols with the next character do so. VV can be replaced by X and IIIII can be replaced by V to give XV in the above. Keep making replacements until you can make no more. Put the symbols in order from largest to smallest symbol and you have your answer.

Now the Romans were obviously a bit lazy as bored with writing even four Is in a row they sometimes introduced a new set of abbreviations, so that IIII became IV and VIIII became IX. Putting a smaller symbol (like I) before a larger one (like X) instead of after meant subtract it to get the number. so IX means “one less than 10” or 9. Counting just got a tiny bit more complicated to get the advantage of writing fewer symbols. Addition now needs a more convoluted algorithm though. There are several ways to do it. The easiest is actually just to change the numbers to add to the simpler form (so IV goes back to IIII). You them do the addition that way, and convert back at the end. Addition just got that little bit harder, and all because of a change in representation.

Worse, doing any more complicated maths is even harder still using the Roman number representation. See if you can work out how to multiply Roman numbers. The Roman number system doesn’t help at all. The only really easy way is to just repeatedly add ( so III x VI is VI + VI + VI). That just isn’t practical for large numbers. Try it on XXIII x LXV1. There are other possible ways including one that is actually based on the binary multiplication algorithms computers use – multiplying and dividing repeatedly by 2. See if you can work out how to do it. Whatever way you do it, its clear that the number system the Romans chose made maths hard for them to do!

A good representation makes maths easy. A bad one makes it much harder to do

Image by Michael Kauer from Pixabay

Luckily, Indian and Arabian scholars understood that the representation they used mattered. They invented, and spread, the Hindu-Arabic numbers and decimal system we use today. What is special about it is that rather than introducing new symbols for bigger and bigger numbers, the position of a symbol is used instead. As we go from nine to ten we go back to the start of our symbols, from 9 back to 0, but stick a 1 in a new 10s column to count how many 10s we have. Counting is still pretty easy but suddenly not only is the algorithm for addition straightforward but we can come up with fairly simple algorithms for multiplication and division too. They are the algorithms you learn at school – though as with any algorithm making sure you follow the steps exactly and don’t miss steps is hard for a human (unlike for a computer). That is why we tend to find learning maths hard at first and it gets easier the more we practice.

In fact Romans needing to do serious maths probably used a variation of an abacus representing numbers with stones. They would do a calculation on the abacus and then convert the answer back into the Roman number system. And guess what. The Roman Abacus uses columns to represent larger numbers in a very similar way to the Hindu-Arabic system. The Romans understood that representation matters too.

Image by Hans from Pixabay

Sometimes things are hard to do just because we make them hard! The secret of coming up with good algorithms is often to come up with a good representation first. In programming too, if you come up with a good way to represent data, a good data structure, you can often then make it much easier to write an efficient program.

This article was first published on the original CS4FN website.

EPSRC supports this blog through research grant EP/W033615/1.

A Godlike Heart

A short story by Rafael Pérez y Pérez of the Universidad Autónoma Metropolitana, México translated from the original Spanish by Paul Curzon, Queen Mary University of London

(From the archive)

Mexican deity Quetzalcoatl
Image by Alexa from Pixabay

Divinity, all the gods and all the forces that man fails to understand, are sources of inspiration, a supreme gift which can be introduced in the heart or movement of men to make them a yoltéotl, a “heart deified”. (Miguel León-Portilla, The Old Mexican, Mexico: FCE, 1995 page 180)

Part I

Allow me a moment, Your Excellency. Now that I’m older, it’s hard to remember. But don’t worry, I will tell the whole story so that your priests can record it.

It all started that afternoon, on the day of Huey Tozoztli, just before the celebration to the maize goddess Centéotl. On the horizon you could see large pools of blood – the result of the endless struggle of the gods maintaining order in the cosmos – which, when mixed with the clouds and rays of sunshine on the background blue of the universe, drenched the sky with reddish, orange and yellow. As usual, I spent most of my free time watching everything that went on in Tlatelolco market.

What most caught my attention amongst that huge convergence of smells, sounds and forms were grasshoppers; not only lovely to eat roasted on a tortilla, but also alive and full of dynamism, sometimes in the air and sometimes on the floor, sometimes in flight and sometimes sluggishly bound to the Earth – watching me. I was mesmerised for hours. I would line them up in rows of three insects, each row identified by a symbol and each grasshopper with its own number. I then watched the various patterns that arose when some reacted and tried to flee, “grasshoppers 1 and 3 in the first row jumped, while grasshopper 2 did not move.” Sometimes they were impossible to control!

That afternoon I came across Donají, the daughter of a famous Jaguar Knight. She wore a shawl across her shoulders so that you could barely see the long necklace of seashells hanging from her neck that, all tangled up, reached to just above her ankles. To see her made my heart begin to beat so, so fast! Although it was not the first time I had seen her, I had never had the opportunity to introduce myself. I stood beside her, but my mouth failed to produce a sound. No doubt she noticed my nervousness. I spent anxious moments just stuttering, until I said, ‘I’m Tizoc’. A grin spread across her face and she continued on her way without a word. She had ignored me! I felt humiliated. Who was Donají to treat me that way! I wanted to run and hide. Despite her arrogance, I felt a great attraction to her; I promised that one day I would show her who Tizoc really was and how wrong she was to treat me that way.

Part II

Several moons passed when one morning I woke up to hear a terrifying story: Donají had been kidnapped by a thug who was sentenced to death! A search was immediately organised, directed by her father, the great Jaguar Knight, which everyone joined. Eight units were formed. I was assigned to the group that went to Coyoacan. Once there, the warrior commanded us to spread out throughout the area in pairs to speed the search of the area. Because of my youth and inexperience I was appointed as an assistant to Sayil, a retired warrior of the Mexican army. We spent the first night by a stream. While looking for some dry branches to make a fire, I kept wondering how Donají would be feeling. After eating some fruit and roasted snake, I decided to distract myself and I started to enjoy my favourite pastime: watching the world! I was absorbed by a group of fireflies: while flying they would disappear without a trace only to then appear from nowhere. They formed groups of flying dancers in the darkness, following the rhythm of imaginary drums with lit torches plugged into their bodies. It seemed like a ceremony executed by priests in honour of some deity. I was completely immersed in my thoughts, admiring the ritual, when I discovered something surprising: fireflies and crickets share an essence! Grasshoppers jump or stand still on the ground; the flying fireflies were lit or unlit. In both cases, part of their behaviour can be described in terms of two states: jumping or landing; lit or unlit. It was what the priests called the divine essence! I was completely absorbed in my thoughts, when a voice interrupted me:

– ‘Tizoc, are you all right?’, asked Sayil.

– ‘I’m watching the fireflies: I want to see what they can communicate to me’, I replied.

– ‘Communicate?’

– ‘See how some fireflies are lit and others are off. Imagine that if two fireflies flying next to each other are on. We are receiving the message: ‘We are happy’. Now, imagine that we have three fireflies, one lit, then another lit but the third not lit. They are wanting to confess to us: “Walk to the lake and you will find a basket full of cocoa”. We both laughed. I continued: ‘We should call this “the behaviour of the two states.”‘

– ‘I once saw a fortune-teller use the same method’, commented Sayil yawning. I listened intently. ‘He had three figurines made of opossum bones representing Tlahuizcalpantecuhtli, the malevolent God of Venus, who fires darts both at people and at other objects, causing bad things to happen. People asked the fortune-teller questions like “Will the harvest be good this year?” Then he put the figurines in a jar and tossed them: he predicted the future based on how many landed on their back and how many fell on their front – or in terms of fireflies, how many were lit and how many unlit – together with the order in which they fell.’

Sayil’s words left me paralysed for a moment: the priests communicated with the deities through messages made of patterns represented as two states! I was excited and shouted:

– ‘I knew that the grasshoppers and fireflies were connected with the gods!’

Sayil didn’t really understand what I was saying, and he was too tired to ask. A few minutes later he fell asleep, though I only went to sleep late in to the night.

Very early the next morning we continued the search. In some thickets we found the necklace of seashells that I had seen Donají wearing in the market. After a while we came to a crossroads; Sayil, despite all his experience, was not sure which way to turn. So I suggested:

– ‘Let’s ask the gods which path is the right one’.

– ‘What do you mean?’

I pulled out a small leather pouch containing three round stones, which the night before I had painted on one side with green dye made from vegetable plants. I had left the other side its natural grey colour. I put them into a jar and threw them so they landed in a line and said:

– ‘If the green painted side is facing up, it is equivalent to a firefly turned on. If the grey side is exposed it is equivalent to an off’.

– ‘You want to play the soothsayer? We don’t know how to interpret the gods!’

– ‘But we can ask them to guide us’, I said.

– ‘How?’ The warrior asked impatiently.

– ‘Assign to each of the five directions of the universe, a pattern in the stones. Implore the gods for their advice and throw them. I am sure the pattern representing the direction that arises will give us the correct way to go. It is the same as it was when the soothsayer asked about the harvest.’ Sayil didn’t seem to understand my idea, so I continued saying: ‘the combination of stones grey-grey-grey represents the centre, that is, stay where we are. Grey-grey-green means walking towards where the nomadic people are, to the north. Grey-green-grey means walk towards the Zapotec lands in the South. Grey-green-green, means walk to where Tonatiuh, the Sun God emerges, and green-grey-grey means walk in the opposite direction.

I clearly remember that Sayil thought this seemed a silly idea. However, time was short and we didn’t have another way to decide which road to take. So, rather than do nothing he decided to go with my idea:

– ‘How will we know how many steps to go?’ He asked now even more impatiently.

– ‘Once we know the direction we go back to throwing stones. There are eight possible patterns.’

– ‘How do you know?’

– ‘Believe me. I spent a long time watching the grasshoppers jumping! Each pattern represents a number from zero to seven. Then, if we get the pattern 0 we move 20 steps; if pattern 1 appears move 40 steps; if 2 appears we move 80 steps, and so on.

– ‘Tizoc, I think you’ve lost your mind’, Sayil said desperately.

– ‘Trust me. So the first throw will be a statement that tells us where to walk. The second will tell us the number of steps forward. We continue doing this until the instruction appears as the green-green-green pattern, which will mean we have received all the directions.

I put the pebbles in a jar, prayed to the gods for help and threw:

– ‘Grey-green-grey. We have to move towards the land of the Zapotecs! Now, let’s see how many steps: green-green-green, it means …2,560 steps’. I went back to throwing the stones: ‘then we head towards where Tonatiuh rises and walk … 640 steps’.

– ‘Tizoc, are you going to spend all morning throwing stones while Donají is about to die? When are you going to finish this?’

– ‘When the gods tell me to.’

I threw the stones again and to Sayil’s surprise the green-green-green combination appeared: end of the message! We followed the instructions sent by our gods and even though I hadn’t been able to make Sayil believe, we did finally find the hideout of the kidnapper.

Donají was inside a small cave whose entrance was blocked; on seeing her my heart began to pound! Unfortunately, a surprise awaited us, we saw that the kidnapper had two accomplices: this complicated things greatly as we would need support for the rescue. We decided Sayil would go for help while I stayed to monitor the situation, so without wasting more time my partner set off.

Near dark I tried to get as close as possible to let Donají know that she would soon be rescued; I was sure she would be glad of my presence. Unfortunately, one of the thugs discovered me. I was immediately thrown into the cave:

– ‘What are you doing here?’ She asked, shocked to see me.

– ‘Donají! Don’t worry; help will be here soon’, I replied, stuttering again! She immediately realised that there was no else out there to rescue us. Her face contorted in anger and she shouted:

– ‘Why didn’t you go in search of my father instead of getting caught!’

She burst into a flood of tears, weeping and weeping for a long time until she finally fell asleep. I felt a failure. But I swore by the gods to get her out of there!

I tried to stay calm when the three thugs approached: first the leader, who was very young; then a burly one, who seemed a bit of an idiot; and finally a slave who, I suppose, had simply taken the opportunity to get away. The idiot and slave dragged me out of the cave and tied me by my wrists to a tree branch. The noise woke up Donají. I was very scared. The leader began to punch me in the stomach. He wanted to know how many people knew the hiding place. I will never give him the information he wants I told myself. He repeatedly punched me until he grew bored. Then he took a leg of venison, clutching the hoof tightly with both hands he crashed it into my nose! I thought I would die! Donají screamed desperately until finally they took me back to the cave.

From the twisted material of her shawl she made presses and bandages. She wiped my face carefully and all my wounds trying to stem the bleeding. She spent the whole night giving me water to drink and mopping my brow. I will never forget her courage and fortitude! Unfortunately, the next morning, things got worse:

– ‘Tizoc, we have to get up.’

– ‘Are we leaving? Where are we going?’

– ‘I overheard them say that we will go to a valley that is a half-day along the path to Totolhuacalco. The sky is cloudy, so surely it will rain later. If we start today, there is no way anyone will work out where we have gone.’

The situation was critical and I had to come up with something before we left …

Part III

The next day, we were already installed in the new hideout, watching our new surroundings when Donají asked:

– ‘What are your thinking about, Tizoc’?

– ‘The gods have sent me a vision’, I answered.

– ‘A vision? What do you mean?’

– ‘Listen: today, at dawn, Sayil arrived with reinforcements to our former hideout, but was surprised to find it abandoned. Now how could he find us? The rain had washed away all traces of our departure. How would he explain to the great Jaguar Knight that he had lost the trail of his daughter? Sayil and the others, now desperate, reviewed the surroundings and, entering the cave where we had stopped, discovered some strange signs.’

– ‘Do you mean the symbols you drew on the wall?’

– ‘That’s right! One of the soldiers said “It looks like a big fly”. Sayil immediately understood the meaning of the drawings and shouted “No, it’s a firefly!”‘

– ‘What are you talking about?’ Donají asked confused.

At that moment we heard loud cries and Sayil, along with a group of Mexica warriors, began the attack on the new hideout. The slave tried to flee, but was captured immediately; the idiot resisted, but the warriors took a stone and split his head in two; the leader tried to attack Donají, but Sayil grabbed him and strangled him. In just a few moments it had all ended for the trio! Donají wept with happiness. My plan had worked! I was ecstatic! I had finally shown to Donají my worth! It was an unforgettable day for me.

How did they find us? Let me explain, Your Excellency, just let me drink a little water … thank you. It all happened as follows. That day I had to devise a way to communicate to Sayil where we were being taken. I was well aware that our lives depended on it, but was paralysed. Unexpectedly, I heard what I thought was a message from the gods: grasshoppers singing! Two states! That was the solution! I estimated the number of steps required to travel half a day along the Totolhuacalco path and using the same code that Sayil and I had used to find Donají, I left the approximate position of our new location on the cave wall! The kidnappers never suspected that those drawings were instructions of how to find us. So Sayil was given the key to finding us! … Thank you, Your Excellency! I know it was ingenious. Thank you very much. Am I sorry? … What do you mean? “What happened to Donají?”… Your question opens old wounds. I think that you and your brothers would never understand what I mean when I say that, although I never saw her again, my heart was forever linked to hers. I’m tired. With your permission, I would like to go to sleep now.

Two states: divine essence! What can they teach us? What wonders can man create with them? Because while enduring the fifth sun, hearts will be deified. (Tizoc)

The End.

More on …

Related Magazines …

EPSRC supports this blog through research grant EP/W033615/1. 

Mary Clem: getting it right

by Paul Curzon, Queen Mary University of London

Mary Clem was a pioneer of dependable computing long before the first computers existed. She was a computer herself, but became more like a programmer.

A tick on a target of red concentric zeros
Image by Paul Curzon

Back before there were computers there were human computers: people who did the calculations that machines now do. Victorian inventor, Charles Babbage, worked as one. It was the inspiration for him to try to build a steam-powered computer. Often, however, it was women who worked as human computers especially in the first half of the 20th century. One was Mary Clem in the 1930s. She worked for Iowa State University’s statistical lab. Despite having no mathematical training and finding maths difficult at school, she found the work fascinating and rose to become the Chief Statistical Clerk. Along the way she devised a simple way to make sure her team didn’t make mistakes.

The start of stats

Big Data, the idea of processing lots of data to turn that data into useful information, is all the rage now, but its origins lie at the start of the 20th century, driven by human computers using early calculating machines. The 1920s marked the birth of statistics as a practical mathematical science. A key idea was that of calculating whether there were correlations between different data sets such as rainfall and crop growth, or holding agricultural fairs and improved farm output. Correlation is the the first step to working out what causes what. it allows scientists to make progress in working out how the world works, and that can then be turned into improved profits by business, or into positive change by governments. It became big business between the wars, with lots of work for statistical labs.

Calculations and cards

Originally, in and before the 19th century, human computers did all the calculations by hand. Then simple calculating machines were invented, so could be used by the human computers to do the basic calculations needed. In 1890 Herman Hollerith invented his Tabulator machine (his company later became computing powerhouse, IBM). The Tabulator machine was originally just a counting machine created for the US census, though later versions could do arithmetic too. The human computers started to use them in their work. The tabulator worked using punch cards, cards that held data in patterns of holes punched in to them. A card representing a person in the census might have a hole punched in one place if they were male, and in a different place if they were female. Then you could count the total number of any property of a person by counting the appropriate holes.

Mary was being more than a computer,
and becoming more like a programmer

Mary’s job ultimately didn’t just involve doing calculations but also involved preparing punch cards for input into the machines (so representing data as different holes on a card). She also had to develop the formulae needed for doing calculations about different tasks. Essentially she was creating simple algorithms for the human computers using the machines to follow, including preparing their input. Her work was therefore moving closer to that of a computer operator and then programmer’s job.

Zero check

She was also responsible for checking calculations to make sure mistakes were not being made in the calculations. If the calculations were wrong the results were worse than useless. Human computers could easily make mistakes in calculations, but even with machines doing calculations it was also possible for the formulae to be wrong or mistakes to be made preparing the punch cards. Today we call this kind of checking of the correctness of programs verification and validation. Since accuracy mattered, this part of he job also mattered. Even today professional programming teams spend far more time checking their code and testing it than writing it.

Mary took the role of checking for mistakes very seriously, and like any modern computational thinker, started to work out better ways of doing it that was more likely to catch mistakes. She was a pioneer in the area of dependable computing. What she came up with was what she called the Zero Check. She realised that the best way to check for mistakes was to do more calculations. For the calculations she was responsible for, she noticed that it was possible to devise an extra calculation, whereby if the other answers (the ones actually needed) have been correctly calculated then the answer to this new calculation is 0. This meant, instead of checking lots of individual calculations with different answers (which is slow and in itself error prone), she could just do this extra calculation. Then, if the answer was not zero she had found a mistake.

A trivial version of this general idea when you are doing a single calculation is to just do it a second time, but in a different way. Rather than checking manually if answers are the same, though, if you have a computer it can subtract the two answers. If there are no mistakes, the answer to this extra check calculation should be 0. All you have to do is to look for zero answers to the extra subtractions. If you are checking lots of answers then, spotting zeros amongst non-zeros is easier for a human than looking for two numbers being the same.

Defensive Programming

This idea of doing extra calculations to help detect errors is a part of defensive programming. Programmers add in extra checking code or “assertions” to their programs to check that values calculated at different points in the program meet expected properties automatically. If they don’t then the program itself can do something about it (issue a warning, or apply a recovery procedure, for example).

A similar idea is also used now to catch errors whenever data is sent over networks. An extra calculation is done on the 1s and 0s being sent and the answer is added on to the end of the message. When the data is received a similar calculation is performed with the answer indicating if the data has been corrupted in transmission. 

A pioneering human computer

Mary Clem was a pioneer as a human computer, realising there could be more to the job than just doing computations. She realised that what mattered was that those computations were correct. Charles Babbages answer to the problem was to try to build a computing machine. Mary’s was to think about how to validate the computation done (whether by a human or a machine).

More on …

Related Magazines …

EPSRC supports this blog through research grant EP/W033615/1.