Victorian Computer Scientists, Ada Lovelace and Charles Babbage were interested in Magic Squares. We know this because a scrap of paper with mathematical doodles and scribbles on it in their handwriting has been discovered, and one of the doodles is a magic square like this one. In a magic square all the rows, columns and diagonals magically add to the same number. At some point, Ada and Charles were playing with magic squares together. Creating magic squares sounds hard, but perhaps not with a bit of algorithmic magic.
The magical effect
For this trick you ask a volunteer to pick a number. Instantly, on hearing it, you write out a personal four by four magic square for them based on that number. When finished the square contents adds to their chosen number in all the usual ways magic squares do. An impressive feat of superhuman mathematical skills that you can learn to do most instantly.
Making the magic
To perform this trick, first get your audience member to select a large two digit number. It helps if it is a reasonably large number, greater than 20, as you’re going to need to subtract 20 from it in a moment. Once you have the number you need to do a bit of mental arithmetic. You need an algorithm – a sequence of steps – to follow that given that number guarantees that you will get a correct magic square.
For our example, we will suppose the number you are given is 45, though it works with any number.
Let’s call the chosen number N (in our example: N is 45). You are going to calculate the following four numbers from it: N-21, N-20, N-19 and N-18, then put them in to a special, precomputed magic square pattern.
The magic algorithm
Sums like that aren’t too hard, but as you’ve got to do all this in your head, you need a special algorithm that makes it really easy. So here is an easy algorithm for working out those numbers.
Image by CS4FN.
Start by working out N – 20. Subtracting 20 is quite easy. For our example number of 45, that is 25. This is our ‘ROOT’ value that we will build the rest from.
N-19. Just add 1 to the root value (ROOT + 1). So 25 + 1 gives 26 for our example.
N-18. Add 2 to the root value (ROOT + 2). So 25 + 2 gives 27.
N-21. Subtract 1 from the root value (ROOT – 1). So 25 – 1 gives 24.
Having worked out the 4 numbers created form the original chosen number, N, you need to stick them in the right place in a blank magic square, along with some other numbers you need to remember. It is the pattern you use to build your magic square from. It looks like the one to the right. To make this step easy, write this pattern on the piece of paper you write the final square on. Write the numbers in light pencil, over-writing the pencil as you do the trick so no-one knows at the end what you were doing.
A square grid of numbers like this is an example of what computer scientists call a data structure: a way to store data elements that makes it easy to do something useful: in this case making your friends think you are a maths superhero.
When you perform this trick, fill in the numbers in the 4 by 4 grid in a random, haphazard way, making it look like you are doing lots of complicated calculations quickly in your head.
Finally, to prove to everyone it is a magic square with the right properties, go through each row, column and diagonal, adding them up and writing in the answers around the edge of the square, so that everyone can see it works.
The final magic square for chosen number 45
So, for our example, we would get the following square, where all the rows, columns and diagonals add to our audience selected number of 45.
Image by CS4FN.
Why does it work?
If you look at the preset numbers in each row, column and diagonal of the pattern, they have been carefully chosen in advance to add up to the number being subtracted from N on those lines. Try it! Along the top row 1 + 12 + 7 = 20. Down the right side 11 + 5 + 4 = 20.
Do it again?
Of course you shouldn’t do it twice with the same people as they might spot the pattern of all the common numbers…unless, now you know the secret, perhaps you can work out your own versions each with a slightly different root number, calculated first and so a different template written lightly on different pieces of paper.
Peter McOwan and Paul Curzon, Queen Mary University of London
By Przemysław Wałęga, Queen Mary University of London
Logical reasoning and proof, whether done using math notation or informally in your head, is an important tool of computer scientists. The idea of proving, however, is often daunting for beginners and it takes a lot of practice to master this skill. Here we look at a simple puzzle to get you started.
Computer Scientists use logical reasoning and proofs a lot. They can be used to ensure correctness of algorithms. Researchers doing theoretical computer science use proofs all the time, working out theories about computation.
Proving mathematical statements can be very challenging, though. Coming up with a proof often requires making observations about a problem and exploiting a variety of different proof methods. Making sure that the proof is correct, concise, and easy to follow matters too, but that in itself needs skill and a lot of practice. As a result, proving can be seen as a real art of mathematics.
Let’s think about a simple puzzle to show how logical thinking can be used when solving a problem. The puzzle can be solved without knowing any specific maths, so anyone can attempt it, but it will probably look very hard to start with.
Before you start working on it though, let me recommend that first you try to solve it entirely in your mind, that is, with no pen and paper (and definitely no computer!).
The Puzzle
Here is the puzzle, which I heard at a New Year’s party from a friend Marcin:
Mrs. and Mr. Taylor hosted a party and invited four other couples. After the party, everyone gathered in the hallway to say their goodbyes with handshakes. No one shook hands with themselves (of course!) or their partner, and no one shook hands with the same person more than once. Each person kept track of how many people they had shaken hands with. At one point, Mr. Taylor shouted “STOP” and asked everyone to say how many people they had shaken hands with. He received nine different answers.
How many people did Mrs Taylor shake hands with?
I will give you some hints to help solving the puzzle, but first try to solve it on you own, and see how far you get. Maybe you will be solve the puzzle on your own?
Why did I recommend solving the puzzle without pen and paper? Because, our goal is to use logical and critical thinking instead of finding a solution in a “brute force” manner, that is, blindly listing all the possibilities and checking each of them to find a solution to the puzzle. As an example of a brute force way of solving a problem, take a crossword puzzle where you have all but one of the letters of a word. You have no idea what the clue is about, so instead you just try the 26 possible letters for the missing one and see which make a word and then check which that do fit the clue!
Notice that the setting of our puzzle is finite: there are 10 people shaking hands, so the number of ways they shake hands is also finite if bigger than say checking 26 different letters of the crossword problem. That means you could potentially list all the possible ways people might shake hands to solve the puzzle. This is, however, not what we are aiming for. We would like to solve the puzzle by analysing the structure of the problem instead of performing brute force computation.
Also, it is important to realise that often mathematicians solve puzzles (or prove theorems) about situations in which the number of possibilities is infinite so the brute force approach of listing them all is not possible at all. There are also many situations where the brute force approach is applicable in theory, but in practice it would require considering too many cases: so many that even the most powerful computers would not be able to provide us with an answer in our lifetimes.
For our puzzle, you may be tempted to list all possible handshake situations between 10 people. Before you do start listing them, let’s check how much time you would need for that. You have to consider every pair that can be formed from 10 people. A mathematician refers to that as “10 choose 2”, the answer to which is that there are 45 possible pairs among 10 people (the first person pairs with 9 others, the next has 8 others to pair with having been paired with the first already, and so on and 9+8+….+1 = 45). However, 45 is not the number that we are looking for. Each of these pairs can either shake hands or not, and we need to consider all those different possibilities. There are 245 such handshake combinations. How big is this number? The number 210 is 1024, so it is approximately 1000. Hence 240=(210)4 (which is clearly smaller than our 245) is approximately 10004 = 1,000,000,000,000 that is, a trillion. Listing a trillion combinations should sound scary to you. Indeed, if you can be quick enough to write each of the trillion combinations in one second, you will spend 31 688 years. Let’s not try this!
Of course, we can look more closely at the description of the puzzle to decrease the number of combinations. For example, we know that nobody shakes hands with their partner, which will already massively reduce the number. However, let’s try to solve the puzzle without using any external memory aids or computational power. Only our minds.
Can you solve it? A key trick that mathematicians and computer scientists use is to break down problems into simpler problems first (decomposition). You may not be able to solve this puzzle straight away, so instead think about what facts you can deduce about the situation instead.
If you need help, start by considering Hint 1 below. If you are still stuck, maybe Hint 2 will help? Answer these questions and you will be a long way to solving the puzzle.
Hints
Mr. Taylor received nine different answers. What are these answers?
Knowing the numbers above, can you work out who is a partner of whom?
No luck in solving the puzzle? Try to spend some more time before giving up! Then read on. If you managed to solve it you can compare your way of thinking with the full solution below.
Solution
First we will answer Hint 1. We can show that the answers received by Mr. Taylor are 0, 1, 2, 3, 4, 5, 6, 7, and 8. There are 5 couples, meaning that there are 10 people at the party (Mr. and Mrs. Taylor + 4 other couples). Each person can shake hands with at least 0 people and at most 8 other people (since there are 10 people, and they cannot shake hands with themselves or their partner). Since Mr. Taylor received nine different answers from the other 9 people, they need to be 0, 1, 2, 3, 4, 5, 6, 7, and 8. This is an important observation which we will use in the second part of the solution.
Next, we will answer Hint 2. Let’s call P0 the person who answered 0, P1 the person who answered 1, …, P8 the person who answered 8. The person with the highest (or the lowest) number of handshakes is a good one to look at first.
Who is the partner of P8? P8 did not shake hands with themselves and with P0 (as P0 did not shake hands with anybody). So P8 had to shake hands with all the other 8 people. Since no one shakes hands with their partner, it follows that P0 is the partner of P8!
Who is the partner of P7? They did not shake hands with themselves, with P0 and with P1, because we already know that P1 shook hands with P8, and they shook hands with only one person. So the partner of P7 can be either P8, P0, or P1. Since P8 and P0 are partners, P7 needs to be the partner of P1.
Following through with this analysis for P6 and P5, we can show that the following are partners: P8 and P0, P7 and P1, P6 and P2, P5 and P3. The only person among P0, … , P8 who is left without a partner is P4. So P4 needs to be Mrs. Taylor, the partner of Mr. Taylor, the one person left who didn’t give a number.
Consequently, we have also showed that Mr Taylor shook hands with 4 people.
Observe that the analysis above does not only provide us an answer to the puzzle, but it also allows us to uniquely determine the handshake setting as presented in the picture below (called a graph by Computer Scientists). Here, people are nodes (circles) and handshakes are represented as edges (lines) in the graph. Red edges correspond to handshakes with P8, blue edges are handshakes with P7, green with P6 and yellow with P5. Partners are located next to each other, for example, Mr. Taylor is a partner with P4.
Image computer generated by Przemysław Wałęga
Large Language Models
Although this article is about logical thinking, and not about tools to solve logic puzzles, it is interesting to see if current AI models are capable of solving the puzzle. As puzzles go it is relatively easy and occurs on the Internet in different settings and languages, so large language models (LLMs) trained on the Internet should be good at solving it. Let’s test them!
I asked ChatGPT-4o and Gemini 1.5 Flash to solve the puzzle. To my surprise, both of them did struggle. They had problems with understanding some parts of the problem formulation and made mathematical mistakes.
ChatGPT seems to wrongly assume that Mr. Taylor answered his own question about the number of handshakes, and so, that each of 10 people announced a different number of handshakes. As follows from our solution of the puzzle, there exists exactly one graph representing the handshake situation. In this graph, the number of handshakes of Mr. and Mrs. Taylor is the same, namely 4. Hence, the additional assumption made by ChatGPT (that each of 10 people had a different number of handshakes) makes the situation described in the puzzle impossible. Interestingly, ChatGPT was able to solve such an impossible puzzle providing a correct answer… Does it mean that ChatGPT has solved the puzzle?
Gemini, in contrast, states that the puzzle cannot be solved without more information such as the order of arrivals. This is clearly wrong. We know how to solve the puzzle and the order of arrivals is actually completely irrelevant to the puzzle!
This small experiment uses basic LLMs and does not aim to draw any conclusions about their capabilities. I am quite certain that one can find an LLM that can solve this simple puzzle without mistakes. However, this experiment aims to emphasise the need for checking AI solutions yourself. To do that you need to gain the skills of doing proof yourself!
In what follows I provide answers obtained from AI models and highlight as bold parts which are wrong assumptions or reasoning.
Solution by ChatGPT:
Key Observations:
There are 10 people in total at the party (5 couples: Mr. and Mrs. Taylor and 4 other couples).
No one shakes hands with their own partner.
No one shakes hands with themselves or the same person more than once.
The handshake answers must be unique and range from 0 to 9 (since there are 10 people, including Mr. and Mrs. Taylor).
Solution:
Since there are 10 people total, the number of handshakes any one person could have ranges from 0 to 9.
If everyone gives a unique answer, it means:
One person shook hands with 0 people.
Another shook hands with 1 person.
Another with 2, and so on, up to 9.
Steps:
The person who shook hands with 9 people: This person shook hands with everyone else, meaning their partner (who doesn’t shake hands with them) must have shaken hands with 0 people.
The person who shook hands with 8 people: This person shook hands with everyone except their partner and the person who shook hands with 0.
By continuing this pattern, we see that for every unique count of handshakes k, the person with k handshakes corresponds to a partner with 9−k handshakes.
Mrs. Taylor’s Handshakes:
Mr. Taylor shouted “STOP” after collecting answers from all 10 people. Since there are 9 different handshake counts, one of those counts must belong to Mrs. Taylor.
Let’s assume Mr. Taylor is among the group and is the one with the maximum or minimum handshakes.
The pairing pattern ensures Mrs. Taylor’s number of handshakes must fall within the range, but based on symmetry of couples logic !
The key is to match couples symmetrically:
If Mr. Taylor gets answers (0, 1, 2,…
Let’s refine the solution:
The possible handshake counts are 0,1,2,…,9, ensuring each number is unique.
The pairing works such that if one person shakes k hands, their partner shakes 9-k hands.
This logic means:
The person who shook 9 hands paired with the person who shook 0.
The person who shook 8 hands paired with the person who shook 1, and so on.
Mrs. Taylor’s Count:
If there are nine unique handshake counts (from 0 to 9), Mrs. Taylor must have shaken 4 hands because her partner, Mr. Taylor, who controls the setup, must fall at the midpoint to allow symmetrical pairing logic.
Solution by Gemini:
Certainly, let’s solve the handshake puzzle!
Understanding the Problem:
We have 10 people at the party (Mr. and Mrs. Taylor, plus 4 other couples).
No one shakes hands with themselves or their partner.
No one shakes hands with the same person more than once.
Each person keeps track of how many handshakes they’ve done.
Mr. Taylor asks everyone how many handshakes they’ve done, and gets 9 different answers.
We need to figure out how many handshakes Mrs. Taylor did.
Let’s Analyze:
The key to solving this is to consider the possible range of handshakes each person could have.
Lowest Possible Handshakes: If someone is the first to arrive and doesn’t shake hands with anyone else, they’ll have 0 handshakes.
Highest Possible Handshakes: The maximum number of handshakes depends on the order of arrivals and who shakes hands with whom. In the most efficient scenario, everyone could shake hands with everyone else except their partner. This would lead to a maximum of 8 handshakes for each person.
Now, let’s consider the 9 different answers:
Since there are 9 different answers, and the minimum is 0, the maximum number of handshakes someone could have is 8.
Let’s think about Mrs. Taylor:
She can’t have 0 handshakes because she would have to shake hands with someone eventually.
She can’t have 8 handshakes because Mr. Taylor would have to have the same number (since they are the only couple).
Therefore, Mrs. Taylor must have shaken hands with a number between 1 and 7.
Unfortunately, without more information about the order of arrivals and who shook hands with whom, we can’t pinpoint the exact number of handshakes Mrs. Taylor did.
Let me know if you’d like to explore a specific scenario with a particular order of arrivals and handshakes to determine Mrs. Taylor’s exact number!
Victorian, William Stanley Jevons was born in Liverpool in 1835. He was famous in his day as an economist and his smashhit book ‘The Coal Question’ drew the nation’s attention to the reduction in Britain’s coal supplies. He was the first economist to raise the issue of the ecological impact of economics.Jevons had other strings to his bow though and one of the strangest for the time if also incredibly forward thinking was his 1869 “logic piano”: a device that looked a little like a piano but that “played” logic.
Jevons was fascinated with logic and reasoning. He believed you could start with one thing (a premise) and from this work through a chain of reasoning to the conclusion. He thought that this could be done for everything. This was based on a principle he espoused of “the substitution of similars”: essentially reasoning based on the idea that “Whatever is true of a thing is true of its like”, For example, If Pharaohs are gods and Rameses is a Pharaoh (so is one of the things “like” a Pharaoh) then you can conclude Rameses is a god. He built on, and combined the ideas of, the Ancient Greeks with the then new ideas of George Boole, that we now call Boolean logic.
Boolean logic is based on a system of algebra using only the values of true and false (or 1 and 0), with operations corresponding to logical operations such as AND and OR that turn true/false values into new true/false values. This is the logic upon which computers are founded. A key idea was that you can abstract away from actual statements about truth in the real world and just replace them with variables that can stand for anything. Boole had laboriously shown using his logic how new abstract facts could be deduced from existing ones. Jevons realised that when reasoning was thought of like this, it became a mechanical process…and that meant a machine could do it.
His contemporary, Charles Babbage had been working on the idea of building mechanical “computers” but Babbage’s fundamental idea was that machines could do calculation. Jevon’s idea was slightly different and more fundamental: that machines could do logical reasoning, deducing new facts from existing ones. This was an idea that eventually came to fruition in the 20th century with the development of theorem provers where computers were programmed to do complex logical reasoning, even working on building up the whole of mathematics by proving ever more theorems from a few starting facts.
So, (with the help of an unknown craftsperson), Jevons set about designing and building his wooden Logic Piano. The idea was that you could put in the premises, the basic facts, by playing the keys of the “piano”. It would then mechanically apply his reasoning rules to discover all conclusions that could be deduced, altering its conclusion with each new fact added, The keys moved rods and levers that made logical facts appear on (or disappear from) the “display” of the machine – essentially facts on the rods appeared in slots cut into the back of the piano.
The kind of logical problem his machine worked with are Syllogisms (see Superhero Syllogisms). They were invented by the Ancient Greeks who were very good at logic. A syllogism is just a common pattern that combines facts where you figure out a conclusion only using the facts supplied, slotted into a template. For example, if we know facts 1 and 2 in the following template (where you can swap in anything for A, B and C) then we can create a new fact as shown.
Image by Paul Curzon
So let’s replace A with the word superheroes, B with fight crime and C with my favourite superhero, Ghost Girl. If we put them in to the template above we get a new “fact” deduced from two existing ones:
Image by Paul Curzon
Image by Paul Curzon
In the piano, a set of rods acted as truth tables, each one giving a true or false values for each variable. So imagine a piano that could deal with two variables A and B. Each of A and B can have two different values true and false, so there are four possibilities (so four rods):
(A, B);
(A, NOT B);
(NOT A, B);
(NOT A, NOT B)
where we write A to mean the assertion A is true and NOT A (or ~A in the picture) to mean A is false. Each rod represents a possible state of the world.
Let’s look at a simple example. Suppose A stands for the statement “Paul is a programmer” and B stands for “Safia is a programmer”, then the possibilities (if we know no specific facts) are
(Paul is a programmer, Safia is a programmer) : (A, B)
(Paul is a programmer, Safia is NOT a programmer) : (A, NOT B)
(Paul is NOT a programmer, Safia is a programmer) : (NOT A, B)
(Paul is NOT a programmer, Safia is NOT a programmer) : (NOT A, NOT B)
Image by Paul Curzon
Each rod in Jevon’s piano had one of the possibilities on, so each rod represented a possible state of the world being reasoned about. At the start all the rods were visible, showing that nothing specific was yet known.
The point is that these represent all possible states of the world about Paul and Safia and whether they are programmers or not. If we know nothing more then all we can say is that all the pairs of facts are a possibility: all are possible states of the world.
The piano worked by essentially leaving displayed or hiding each rod’s state as new facts were keyed in. (See the video at the end which includes a detailed explanation by expert David E Dunning on the detail of how it did this step by step). Initially all the possibilities are displayed as above. If we add a new fact that we have discovered or wish to assume, say that “Safia IS a programmer” (in terms of the piano, press the B key corresponding to the fact B is true), then doing so removes all states of the world where Safia is NOT a programmer. The piano, therefore, hides all the rods that include the assertion representing “Safia is NOT a programmer” (all those with (NOT B) on them) . We are left with two alternatives:
Image by Paul Curzon
(Paul is a programmer, Safia is a programmer) : (A, B)
(Paul is NOT a programmer, Safia is a programmer) : (NOT A, B)
The mechanics of the machine meant that those facts would remain a possibilities (reading down the rods) but pushing the keys for that assertion would have moved the other rods, so hide their state. In doing so, the piano has deduced from the fact B that the possible conclusions are A AND B is true or NOT A AND B is true.
With three variables instead of two the machine would be able to deal with more complex situations – there are then 8 possibilities so 8 rods representing the 8 different states. .
Image by Paul Curzon
Let A represent superheroes, (so NOT A represents those people who are not superheroes), B represents those people who fight crime and C with a person being Ghost Girl. Suppose we are considering some, at the moment, random person we know nothing about. The possibilities about them are:
(Is a superhero, does fight crime, is Ghost Girl) : (A, B, C)
(Is a superhero, does fight crime, is NOT Ghost Girl) : (A, B, NOT C)
(Is a superhero, does NOT fights crime, is Ghost Girl) : (A, NOT B, C)
(Is a superhero, does NOT fight crime, is NOT Ghost Girl) : (A, NOT B, NOT C)
(Is NOT a superhero, does fight crime, is Ghost Girl) : (NOT A, B, C)
(Is NOT a superhero, does fight crime, is NOT Ghost Girl) : (NOT A, B, NOT C)
(Is NOT a superhero, does NOT fights crime, is Ghost Girl) : (NOT A, NOT B, C)
(Is NOT a superhero, does NOT fight crime, is NOT Ghost Girl) : (NOT A, NOT B, NOT C)
If we put the fact about them into the piano that ALL superheroes fight crime (ALL A are B) then we remove all rods where A is true but B is different so false (a superhero who doesn’t fight crime) as in this world, that is impossible.
Image by Paul Curzon
(Is a superhero, does fight crime, is Ghost Girl) : (A, B, C)
(Is a superhero, does fight crime, is NOT Ghost Girl) : (A, B, NOT C)
(Is NOT a superhero, does fight crime, is Ghost Girl) : (NOT A, B, C)
(Is NOT a superhero, does fight crime, is NOT Ghost Girl) : (NOT A, B, NOT C)
(Is NOT a superhero, does NOT fights crime, is Ghost Girl) : (NOT A, NOT B, C)
(Is NOT a superhero, does NOT fight crime, is NOT Ghost Girl) : (NOT A, NOT B, NOT C)
Then we add the fact that Ghost Girl is a superhero (C is a A) so remove all those rods where Ghost Girl is not a superhero (ie NOT A, C):
Image by Paul Curzon
(Is a superhero, does fight crime, is Ghost Girl) : (A, B, C)
(Is a superhero, does fight crime, is NOT Ghost Girl) : (A, B, NOT C)
(Is NOT a superhero, does fight crime, is NOT Ghost Girl) : (NOT A, B, NOT C)
(Is NOT a superhero, does NOT fight crime, is NOT Ghost Girl) : (NOT A, NOT B, NOT C)
We have deduced (the first possible state) that if the person we are interested in is Ghost girl then she is a superhero. We are also left with other possibilities too. If the person we are considering is not actually Ghost Girl then they may or may not fight crime and may or may not be a superhero!
If we add in an additional fact that the person we are thinking of IS actually Ghost Girl then we remove those extra rods so possibilities and get
Image by Paul Curzon
(Is a superhero, does fight crime, is Ghost Girl) : (A, B, C)
Ghost Girl is a superhero who does fight crime! We knew she was Ghost Girl and was a superhero but using the piano we have now deduced that she does fight crime. The machine has deduced the syllogism we gave at the start.
IF ALL superheroes fight crime AND
Ghost girl is a superhero
THEN
Ghost girl fights crime.
The actual piano dealt with 4 variables (A, B, C, D) so had 16 rods representing the 16 different combinations. It also included keys to indicate the end of a conjecture, a key for IS A, and more to allow specific assertions to be input. The mechanism then hid rods automatically based on the facts entered. To use it, you did as we did: create a table of what A, B, C and D stand for (this is done outside the machine), enter the facts you want to reason about, and it then displayed all the possible states that remained in terms of A, B, C and D. Then, by seeing what each of the variables stood for in the table, you could convert that answer back into a deduced fact about the real world that you were interested in.
Amazingly, (after a first failed attempt) it did work. It is similar in idea to modern day theorem provers which are used to verify properties of safety-critical computer designs that must npot have bugs. Of course, being small and woody, the logic piano couldn’t solve every thing but then it turns out that was always an impossible dream. Even modern computers (and human mathematicians) have fundamental limits in what they can do (which is another story). The logic piano was a rather amazing, if woody, start to the area of automated theorem proving, though.
– Paul Curzon, Queen Mary University of London
Make a paper logic piano
Here is a kit to make a paper or card logic piano of your own (actually more like Jonons’ logic abacus the piano was a mechanised version of):
A Talk by David E Dunning at the Imagining AI conference about William Stanley Jevons and the logic piano including at the end a more detailed explanation of how pressing keys actually caused rods to by hidden in a series of steps. See also his article about it for the Computer History Museum.
It is Red nose day in the UK the day of raising money for the comic relief charity by buying and wearing red noses and generally doing silly things for money.
Red noses are not just for red nose day though and if you ‘ve been supporting it every year, you possibly now have a lot of red noses like we do. What can you do with lots of red noses? Well one possibility is to count in red nose binary as a family or group of friends. (Order your red noses (a family pack has 4 or a school pack 25) from comic relief or make a donation to the charity there.)
Image by CS4FN
Red nose binary
Let’s suppose you are a family of four. All stand in a line holding your red noses (you may want to set up a camera to film this). How many numbers can 4 red noses represent? See if you can work it out first. Then start counting:
No one wearing a red nose is 0,
the rightmost end person puts theirs on for 1,
they take it off and the next person puts theirs on for 2,
the first person puts theirs back on for 3,
the first two people take their noses off and the third person puts theirs on for 4
and so on…
The pattern we are following is the first (rightmost end) person changes their nose every time we count. The second person has the nose off for 2 then on for the next 2 counts. The third person changes theirs every fourth count (nose off for 4 then on for 4) and the last person changes theirs every eighth count (off for 8, on for 8). That gives a unique nose pattern every step of the way until eventually all the noses are off again and you have counted all the way from 0 to 15. This is exactly the pattern of binary that computers use (except they use 1s and 0s rather than wear red noses).
What is the biggest number you get to before you are back at 0? It is 15. Here is what the red nose binary pattern looks like.
Image by CS4FN
Try and count in red nose binary like this putting on and taking off red noses as fast as you can, following the pattern without making mistakes!
The numbers we have put at the top of each column are how much a red nose is worth in that column. You could write the number of the column on that person’s red nose to make this obvious. In our normal decimal way of counting, digits in each column are worth 10 times as much (1s 10s 100s, 1000s, etc) Here we are doing the same but with 2s (1s 2s 4s 8s etc). You can work out what a number represents just by adding that column number in if there is a red nose there. You ignore it if there is no red nose. So for example 13 is made up of an 8s red nose + a 4s red nose + a 1s red nose. 8 + 4 + 1 = 13.
Image by CS4FN
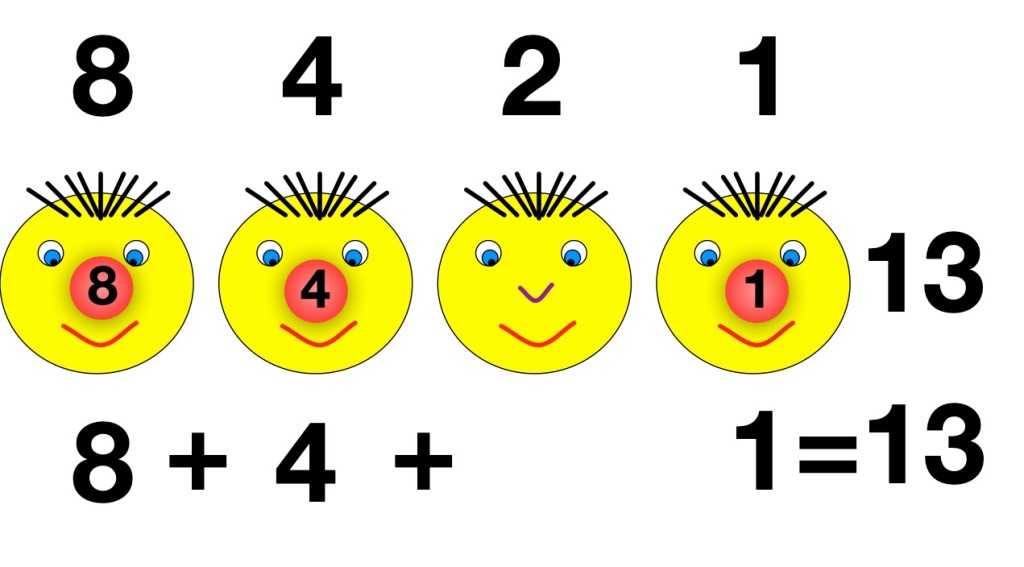
Add one more person (perhaps the dog if they are a friendly dog willing to put up with this sort of thing) with a red nose (now worth 16) to the line and how many more numbers does that now mean you can count up to? Its not just one more. You can now go through the whole original sequence twice once with the dog having no red nose, once with them having a red nose. So you can now count all the way from 0 to 31. Each time you add a new person (or pet*, though goldfish don’t tend to like it) with a red nose, you double the number you can count up to.
There is lots more you can do once you can count in red nose binary. Do red nose binary addition with three lines of friends with red noses, representing two numbers to add and compute the answer on the third line perhaps… for that you need to learn how to carry a red nose from one person to the next! Or play the game of Nim using red nose binary to work out your moves (it is the sneaky way mathematicians and computer scientists use to work out how to always win). You can even build a working computer (a Turing Machine) out of people wearing red noses…but perhaps we will save that for next year.
What else can you think of to do with red nose binary?
*Always make sure your pet (or other family member) has given written consent before you put a red nose on them for ethical counting.
There are several Pi Day’s (14 March: 3.14; 22 July: 22/7) so we should look at how on earth you compute a number like Pi (3.1.4159….). It has an infinite number of digits containing no repeating pattern so you can never tie it down exactly. One of my favourite ways for calculating pi was first devised by the Indian mathematician Mādhava of Sangamagrāma 600 years ago. He worked out an algorithm for working out Pi based on the maths of infinite series that he had also worked out.
Pi is one of the most useful numbers in all of maths. In school you come across it when working out the area or circumference of a circle, but it crops up all over the place including in practical computer science situations. Digital music, for example, relies on it deep down. Remember that the next time you stream your favourite music!
So how, 600 years ago did Mādhava manage to work out a much more accurate version of Pi than anyone before him? He had worked out that certain sequences of infinite numbers wouldn’t get bigger and bigger but would just get closer and closer to some specific number. In particular, he worked out one such sequence linked to pi.
π / 4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 – …
Writing this a slightly different way it gives us a way of calculating pi itself
π = 4 – 4/3 + 4/5 – 4/7 + 4/9 – …
With an infinite number of terms, this gives an accurate value for pi. We can’t add an infinite number of numbers together though. Instead, we can use it to get a good answer. To get an approximation to pi we just follow an algorithm where we gradually add / subtract the next term. Each new calculation then gives us a better estimate of what pi is.
So to start with we just take the first term which says
π = 4 (very approximately)
That isn’t very good as it doesn’t get any digits right! Pi is closer to 3 than to 4. So its not looking hopeful! That doesn’t matter though as it is just a starting point. When we subtract the next term it gets a bit better
π = 4 – 4/3 = 2.6666…
Hmm. Now we have overshot the other way. However, we are closer to the real value of pi than we were. So don’t lose heart, keep going and add the next term
π = 4 – 4/3 + 4/5 = 3.46666…
And another term …
π = 4 – 4/3 + 4/5 – 4/7 = 2.895 …
And another term …
π = 4 – 4/3 + 4/5 – 4/7 + 4/9 = 3.339…
and so on.
The important thing to notice is that after each term included we get a more accurate answer, and we can keep adding terms for as long as we are happy to do the calculations. Mādhava (or his followers) obviously liked doing calculations so kept going until he had worked out pi accurate to 10 decimal places (3.1415926535…) : a new world record at the time beating the previous best of 6 decimal places by a Chinese astronomer Zhao Youqin using a different algorithm, That record had been set 80 years earlier but was smashed by 4 decimal places. This new record lasted for another 96 years. In doing these calculations Mādhava was acting as a ‘computer’ in the original meaning of the word: a human following an algorithm to do computation.
His algorithm is what computer scientists call an iterative algorithm. This kind of algorithm is used quite a lot by computer scientists as it gives a general way of getting a good enough (if not perfect) answer to a problem that otherwise is hard (or impossible) to get a perfect answer to in a reasonable time. You start with a good guess and then gradually refine the answer until you are happy that it is accurate enough. These algorithms can be straightforward to code as it is just running a loop doing calculations that refine the answer. Mādhava was happy with 10 decimal places of accuracy but he could have kept going. The trouble is this is a very slow algorithm. As we saw with the first few iterations above, it takes a long time even to home in on the first digit being 3! Every new digit took a lot of extra work to get right. When calculating machines and then computers were invented it became easier to use slow algorithms like this, but even with a faster computer it is still better to have a faster algorithm. Now far faster algorithms have been invented and the world record at the time of writing gives pi accurate to 105,000,000,000,000 decimal places!
Mādhava would have needed to really like doing calculations (and have discovered the secret to eternal life) to have calculated pi that accurately. 600 years ago his world record for pi was still an amazing achievement.
cs4fn 