Category: Algorithmic thinking

Exploring mazes, inventing algorithms (part I) 

by Paul Curzon, Queen Mary University of London

A maze with mouse searching for cheese.

Computer science research in part involves inventing new algorithms or improving new ones. But what does that mean. Let’s explore some mazes to explore algorithms.

What does computer science research involve? It is very varied: from interviewing people to find out what the real problems that need solving in their lives or jobs are; to running experiments to find out what works and what doesn’t; to writing programs to solve problems.

Improving algorithms

A core part of much research is coming up with new and better algorithms that solve particular problems. The kind of algorithm could be anything from a new more secure cryptographic protocol, or a better way to rank the results of a search engine, to a new more effective machine learning algorithm that is less likely to make things up, or perhaps can better explain how it came to its conclusions.

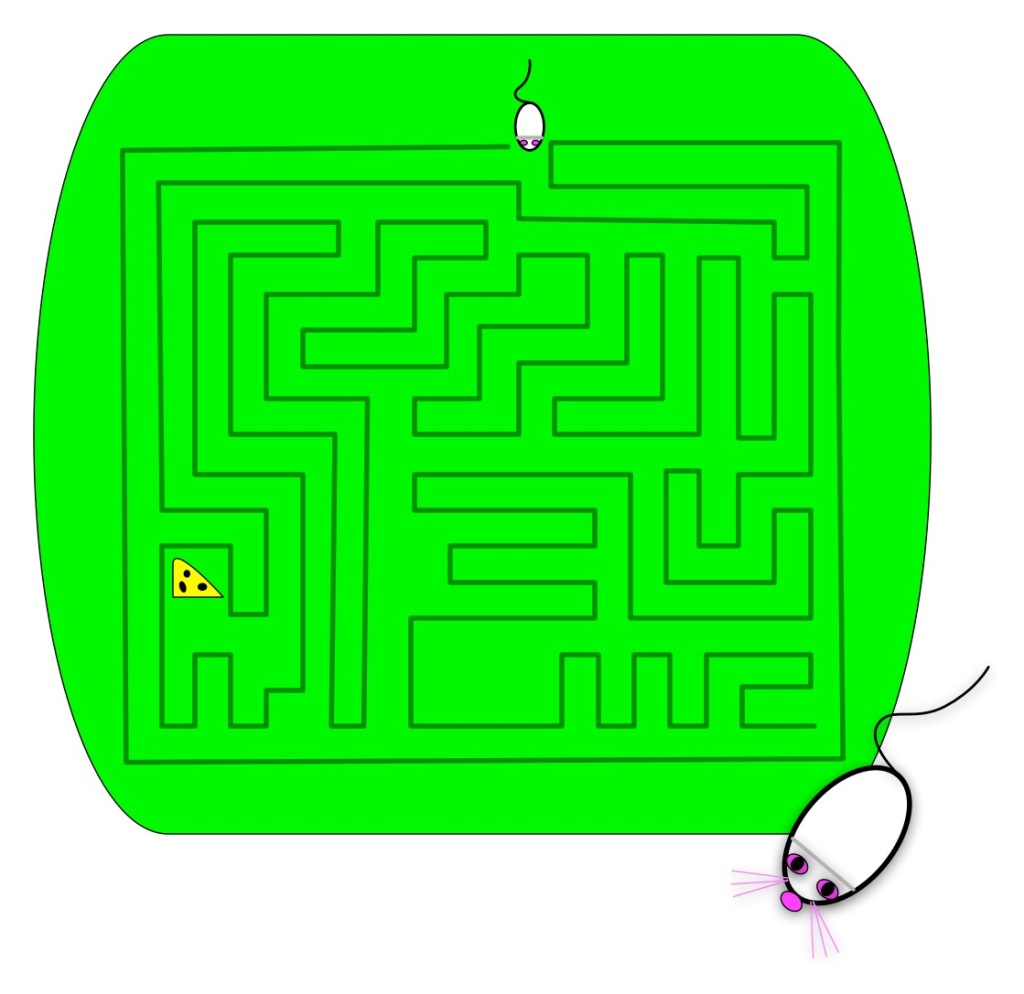
What does it mean to come up with a better algorithm though? Once a problem is solved, isn’t it solved? Let’s explore a simple problem to see. Let’s explore mazes. Solve the simple maze puzzle above before you go on. Find a route that gets the mouse to the cheese.

Wandering around mazes, finding algorithms

If you’ve ever been in a hedge maze in the garden of some stately home, or a corn field maze, the chances are you just dived in and wandered rather aimlessly. Perhaps you tried to remember which way you went at each junction, to avoid going down the same dead-ends more than once. How about solving the paper version of a maze puzzle like the one above? Now perhaps you looked ahead to spot dead-ends to avoid tracing wrong paths with your pencil.

Probably what you are doing is at least a little random. You could, in theory at least, end up going back over the same paths, never taking the right one and and never getting to the middle. Could we come up with an algorithm that guarantees to solve mazes? To be an algorithm it would need to guarantee you ended up finding a path to the centre of the maze if you followed the steps of the algorithm precisely. It should also work for any maze, or at least all mazes of a particular kind. Ideally, the algorithm gives you a path that can then be followed by anyone without them having to run the algorithm themselves. They can just follow the path generated by the algorithm for that maze.

Wall-following

In fact lots of maze algorithms have been invented. Perhaps the one most people have heard of, if they know of any maze algorithm, is called Wall-following. It is very simple to do, You just pick a wall at the entrance either to the left or right and then follow it, If in a garden maze, keep your hand on the hedge as you walk round. If doing a paper puzzle, draw the path sticking to the chosen wall. Try it on the following simple maze.

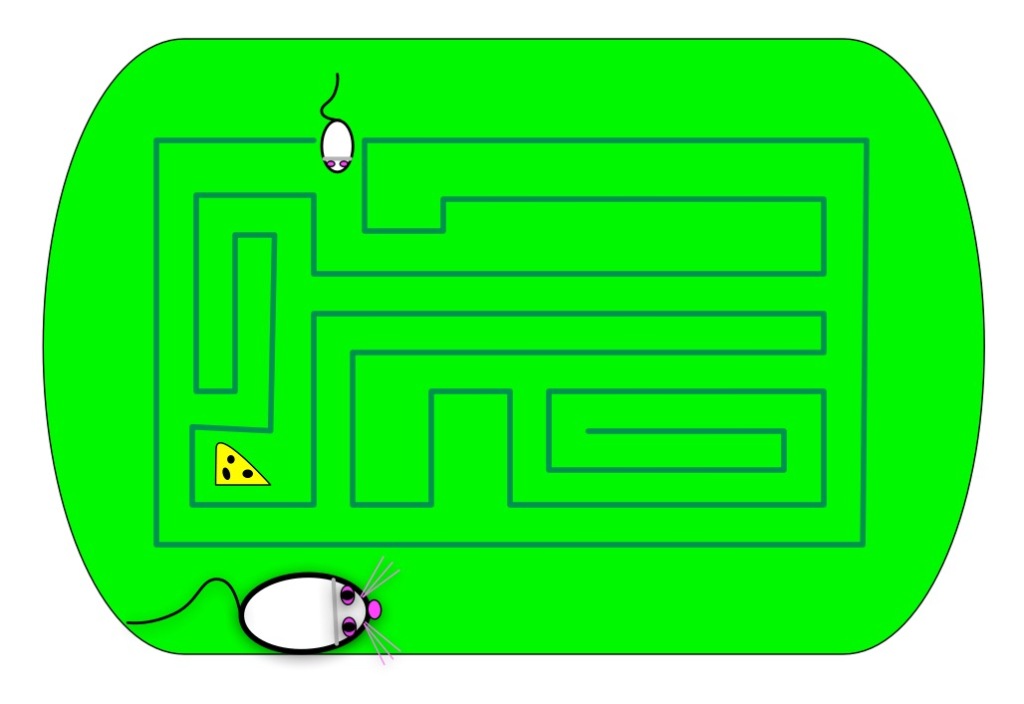
A simple maze with mouse and cheese.

Simply connected

The wall-following algorithm will guarantee to get you to the centre of the maze, and back out again too, but only as long as the maze is what is called simply connected. That just means the maze is constructed from a single hedge (or one unbroken drawn line) not a series of unconnected hedges. If you look at both examples above you will see I created them by just drawing a single wiggly line.

If a maze is simply connected then it cannot have looping paths, so no going round in circles for ever. It will also only have one entrance/exit. That shows the first aspect of inventing algorithms that is important. They often only work for some situations, not all. You must be sure you know what situations they do and don’t work.

Often the earliest algorithms invented to solve a problem are like wall-following: they only work for simple situations. Other people then come along and find new algorithms that can cover more problems (here more mazes). Can you tweak the wall-following maze algorithm to work even if there are multiple exits from the maze, for example? As it stands our algorithm could just take you from the entrance straight out of another exit without exploring much of the maze at all! See the end for one simple way to tweak the algorithm. What if there are paths that take you round in circles? Can you come up with an algorithm to deal with that?

Some times the improvements invented just involve tweaking an existing algorithm as with dealing with multiple exits in a maze. Some times a whole new algorithm is needed.

Faster, higher, stronger?

Even for a simple constrained version of the problem, like simply connected mazes, people can invent better algorithms. What does better mean for a maze? Well one way you might have a better algorithm is if it is faster in coming up with a solution. Another is that the solution it comes up with is faster. For a maze that means a shorter (ideally the shortest) path to the centre. Wall following may get you in to the centre (and out again) but you probably will have discovered a very long path that takes you in and out of lots of dead-ends needlessly. You do find a path to the centre, but it may be a very long path. Can you come up with an algorithm that finds shorter paths?

We will explore an algorithm that does next.

More to come…

Some solutions

The result of wall following on our simple maze

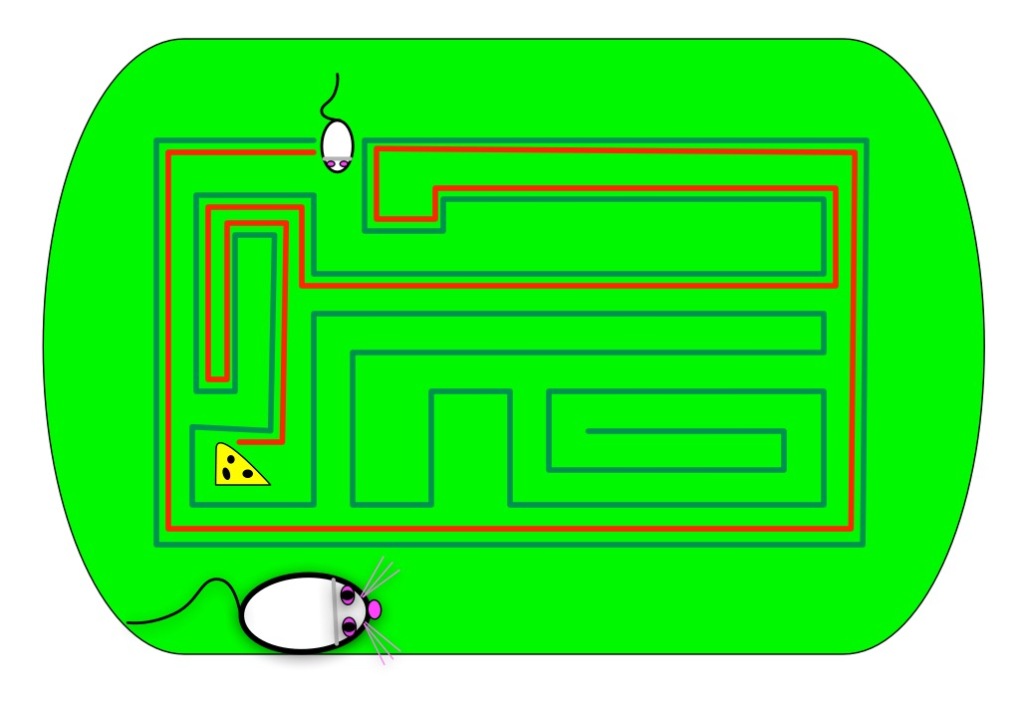
A route for the mouse to follow that takes it to the cheese.

One way to deal with multiple exits

To deal with a maze that has multiple exits, so multiple breaks in the outer wall, tweak the wall-following algorithm as follows. First mark the exit you use to enter the maze, so you know when you return to it. If you come to any other exit then pretend there is a gate there and keep following the wall as though it were unbroken and there were no exit.

More on …

Magazines …

EPSRC supports this blog through research grant EP/W033615/1. 

How does Santa do it?

Fast yuletide algorithms to visit all those chimneys in time

by Paul Curzon, Queen Mary University of London

Lots of Santas in a line
Image by Thomas Ulrich from Pixabay 

How does Santa do it? How does he visit all those children, all those chimneys, in just one night? My theory is he combines a special Scandinavian super-power with some computational wizardry.

There are about 2 billion children in the world and Santa visits them all. Clearly he has magic (flying reindeer remember) to help him do it but what kind of magic (beyond the reindeer)? And is it all about magic? Some have suggested he stops time, or moves through other dimensions, others that he just travels at an amazingly fast speed (Speedy Gonzales or The Flash style). Perhaps though he uses computer science too (though by that I don’t mean computer technology, just the power of computation).

The problem can be thought of as a computational one. The task is to visit, let’s say a billion homes (assuming an average of 2 children per household), as fast as possible. The standard solution assumes Santa visits them one at a time in order. This is what is called a linear algorithm and linear algorithms are slow. If there are n pieces of data to process (here, chimneys to descend) then we write this as having efficiency O(n). This way of writing about efficiency is called Big-O notation. O(n) just means as n increases the amount of work increases proportionately. Double the number of children and you double the workload for Santa. Currently the population doubles every 60 or 70 years or so, so clearly Santa needs to think in this way or he will eventually fail keep up, whatever magic he uses.

Perhaps, Santa uses teams of Elves as in the film Arthur Christmas, so that at each location he can deliver say presents to 1000 homes at once (though then it is the 1000 Elf helpers doing the delivering not Santa which goes against all current wisdom that Santa does it himself). It would speed things up apparently enormously to 1000 times faster. However, in computational terms that barely makes a difference. It is still a linear order of efficiency: it is still O(n) as the work still goes up proportionately with n. Double the population and Santa is in trouble still as his one night workload doubles too. O(2n) and O(1000n) both simplify to mean exactly the same as O(n). Computationally it makes little difference, and if their algorithms are to solve big problems computer scientists have to think in terms of dealing with data doubling, doubling and doubling again, just like Santa has had to over the centuries.

Divide and Conquer problem solving

When a computer scientist has a problem like this to solve, one of the first tools to reach for is called Divide and Conquer problem solving. It is a way of inventing lightening fast algorithms, that barely increase in work needed as the size of the problem doubles. The secret is to find a way to convert the problem into one that is half the size of the original, but (and this is key) that is otherwise exactly the same problem. If it is the same problem (just smaller) then that means you can solve those resulting smaller problems in the same way. You keep splitting the problem until the problems are so small they are trivial. That turns out to be a massively fast way to get a job done. It does not have to be computers doing the divide and conquer: I’ve used the approach for sorting piles of hundreds and hundreds of exam scripts into sorted order quickly, for example.

My theory is that divide and conquer is what Santa does, though it requires a particular superhero power too to work in his context, but then he is magical, so why not. How do I think it works? I think Santa is capable of duplicating himself. There is a precedent for this in the superhero world. Norse god Loki is able to copy himself to get out of scrapes, and since Santa is from the same part of the world it seems likely he could have a similar power.

If he copied himself twice then one of him could do the Northern Hemisphere and the other the Southern hemisphere. The problem has been split into an identical problem (delivering presents to lots of children) but that is half the size for each Santa (each has only half the world so half as many children to cover). That would allow him to cover the world twice as fast. However that is really no different to getting a couple of Elves to do the work. It is still O(n) in terms of the efficiency the work is done. As the population doubles he quickly ends up back in the same situation as before: too much work for each Santa. Likewise if he made a fixed number of 1000 copies of himself it would be similar to having 1000 Elves doing the deliveries. The work still increases proportional to the number of deliveries. Double the population and you still double the time it takes.

Double Santa and double again (and keep doubling)

So Santa needs to do better than that if he is to keep up with the population explosion. But divide and conquer doesn’t say halve the problem once, it says solve the new problem in the same way. So each new Santa has to copy themselves too! As they are identical copies to the original surely they can do that as easily as the first one could. Those new Santas have to do the same, and so on. They all split again and again until each has a simple problem to solve that they can just do. That might be having a single village to cover, or perhaps a single house. At that point the copying can stop and the job of delivering presents actually done. Each drops down a chimney and leaves the presents. (Now you can see how he manages to eat all those mince pies too!)

An important thing to remember is that that is not the end of it. The world is now full of Santas. Before the night is over and the job done, each Santa has to merge back with the one they split from, recursively all the way back to the original Santa. Otherwise come Christmas Day we wouldn’t be able to move for Santas. Better leave 30 minutes for that at the end!

Does this make a big difference? Well, yes (as long as all the copying can be done quickly and there is an organised way to split up the world). It makes a massive difference. The key is in thinking about how often the Santas double in number, so how often the problem is halved in size.

We start with 1 Santa who duplicates to 2, but now both can duplicate to 4, then to 8, 16, and after only 5 splittings there are already 32 Santas, then 64, 128, 256, 512 Santas, and after only 10 splittings we have over a 1000 Santas (1024 to be precise). As we saw that isn’t enough so they keep splitting. Following the same pattern, after 20 splittings we have over a million Santas to do the job. After only 30 rounds of splittings we have a billion Santas, so each can deal with a single family: a trivial problem for each.

So if a Santa can duplicate himself (along with the sleigh and reindeer) in a minute or so (Loki does it in a fraction of a second so probably this is a massive over-estimate and Santa can too), we have enough Santas to do the job in about half an hour, leaving each plenty of time to do the delivery to their destination. The splitting can also be done on the way so each Santa travels only as far as needed. Importantly this splitting process is NOT linear. It is O(log2 n) rather than O(n) and log2 n is massively smaller than n for large n. It means if we double the population of households to visit due to population explosion, the number of rounds of splitting does not need to double, the Santas just have to do one more round of splitting to cover it. The calculation log2 n (the logarithm to base 2 of n) is just a mathematicians way of saying how many times you can halve the number n before you get to 1 (or equivalently how many times you double from 1 before you get up to n). 1024 can be halved 10 times so (log2 1024) is 10. A billion can be halved about 30 times so (log2 1 billion) is about 30. Instead of a billion pieces of work we do only 30 for the splitting. Double the chimneys to 2 billion and you need only one more for a total of 31 splittings.

In computer terms divide and conquer algorithms involve methods (ie functions / procedures) calling themselves multiple times. Each call of the method, works on eg half the problem. So a method to sort data might first divide the data in half. One half is passed to one new call (copy) of the same method to sort in the same way, the other half is passed to the other call (copy). They do the same calling more copies to work on half of their part of the data, until eventually each has only one piece of data to sort (which is trivial). Work then has to be done merging the sorted halves back into sorted wholes. A billion pieces of data are sorted in only 30 rounds of recursive splitting. Double to 2 billion pieces of data and you need just 1 more round of splitting to get the sorting done.

Living in a simulation

If this mechanism for Santa to do deliveries all still seems improbable then consider that for all we know the reality of our universe may actually be a simulation (Matrix-like) in some other-dimensional computer. If so we are each just software in that simulation, each of us a method executing to make decisions about what we do in our virtual world. If that is the nature of reality, then Santa is also just a (special yuletide) software routine, and his duplicating feat is just a method calling itself recursively (as with the sort algorithm). Then the whole Christmas delivery done this way is just a simple divide and conquer algorithm running in a computer…

Given the other ways suggested for Santa to do his Christmas miracle seem even more improbable, that suggests to me that the existence of Santa provides strong evidence that we are all just software in a simulation. Not that that would make our reality, or Christmas, any less special.

More on …

This blog is funded through EPSRC grant EP/W033615/1.