Tag: Charles Babbage

Hear and … their magic square

A magic three by three square with the numbers 2, 9 and 4 in the top row, 7, 5 and 3 in the middle row and 6, 1 and 8 in the bottom row. Each row, column and the two diagnonals add up to 15.
Image by CS4FN

Victorian Computer Scientists, Ada Lovelace and Charles Babbage were interested in Magic Squares. We know this because a scrap of paper with mathematical doodles and scribbles on it in their handwriting has been discovered, and one of the doodles is a magic square like this one. In a magic square all the rows, columns and diagonals magically add to the same number. At some point, Ada and Charles were playing with magic squares together. Creating magic squares sounds hard, but perhaps not with a bit of algorithmic magic.

The magical effect

For this trick you ask a volunteer to pick a number. Instantly, on hearing it, you write out a personal four by four magic square for them based on that number. When finished the square contents adds to their chosen number in all the usual ways magic squares do. An impressive feat of superhuman mathematical skills that you can learn to do most instantly.

Making the magic

To perform this trick, first get your audience member to select a large two digit number. It helps if it is a reasonably large number, greater than 20, as you’re going to need to subtract 20 from it in a moment. Once you have the number you need to do a bit of mental arithmetic. You need an algorithm – a sequence of steps – to follow that given that number guarantees that you will get a correct magic square.

For our example, we will suppose the number you are given is 45, though it works with any number.

Let’s call the chosen number N (in our example: N is 45). You are going to calculate the following four numbers from it: N-21, N-20, N-19 and N-18, then put them in to a special, precomputed magic square pattern.

The magic algorithm

Sums like that aren’t too hard, but as you’ve got to do all this in your head, you need a special algorithm that makes it really easy. So here is an easy algorithm for working out those numbers.

This four by four magic square contains the calculations needed to install the numbers in the correct positions so that the magic square will work with any large two digit number
Image by CS4FN.
  1. Start by working out N – 20. Subtracting 20 is quite easy. For our example number of 45, that is 25. This is our ‘ROOT’ value that we will build the rest from.
  2. N-19. Just add 1 to the root value (ROOT + 1). So 25 + 1 gives 26 for our example.
  3. N-18. Add 2 to the root value (ROOT + 2). So 25 + 2 gives 27.
  4. N-21. Subtract 1 from the root value (ROOT – 1). So 25 – 1 gives 24.
  5. Having worked out the 4 numbers created form the original chosen number, N, you need to stick them in the right place in a blank magic square, along with some other numbers you need to remember. It is the pattern you use to build your magic square from. It looks like the one to the right. To make this step easy, write this pattern on the piece of paper you write the final square on. Write the numbers in light pencil, over-writing the pencil as you do the trick so no-one knows at the end what you were doing.

A square grid of numbers like this is an example of what computer scientists call a data structure: a way to store data elements that makes it easy to do something useful: in this case making your friends think you are a maths superhero.

When you perform this trick, fill in the numbers in the 4 by 4 grid in a random, haphazard way, making it look like you are doing lots of complicated calculations quickly in your head.

Finally, to prove to everyone it is a magic square with the right properties, go through each row, column and diagonal, adding them up and writing in the answers around the edge of the square, so that everyone can see it works.

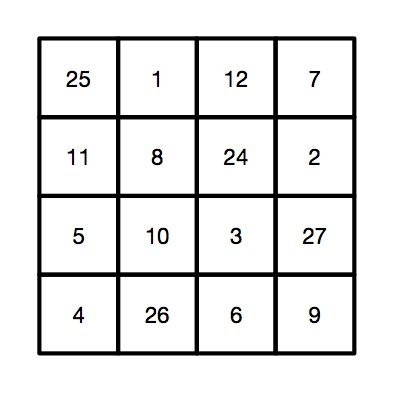
The final magic square for chosen number 45

So, for our example, we would get the following square, where all the rows, columns and diagonals add to our audience selected number of 45.

This four by four magic square is the result of taking the chosen number 45 and performing the sequence of calculations (the algorithm) using it as 'N'.
Image by CS4FN.

Why does it work?

If you look at the preset numbers in each row, column and diagonal of the pattern, they have been carefully chosen in advance to add up to the number being subtracted from N on those lines. Try it! Along the top row 1 + 12 + 7 = 20. Down the right side 11 + 5 + 4 = 20.

Do it again?

Of course you shouldn’t do it twice with the same people as they might spot the pattern of all the common numbers…unless, now you know the secret, perhaps you can work out your own versions each with a slightly different root number, calculated first and so a different template written lightly on different pieces of paper.

Peter McOwan and Paul Curzon, Queen Mary University of London

Related Magazine …

Download our free magic booklets

Magic
Magic

Ada Lovelace: Visionary

It is 1843, Queen Victoria is on the British throne. The industrial revolution has transformed the country. Steam, cogs and iron rule. The first computers won’t be successfully built for a hundred years. Through the noise and grime one woman sees the future. A digital future that is only just being realised.

Red floating treble clef
Image by Gerd Altmann from Pixabay

Ada Lovelace is often said to be the first programmer. She wrote programs for a designed, but yet to be built, computer called the Analytical Engine. She was something much more important than a programmer, though. She was the first truly visionary person to see the real potential of computers. She saw they would one day be creative.

Charles Babbage had come up with the idea of the Analytical Engine – how to make a machine that could do calculations so we wouldn’t need to do it by hand. It would be another century before his ideas could be realised and the first computer was actually built. As he tried to get the money and build the computer, he needed someone to help write the programs to control it – the instructions that would tell it how to do calculations. That’s where Ada came in. They worked together to try and realise their joint dream, jointly working out how to program.

Ada also wrote “The Analytical Engine has no pretensions to originate anything.” So how does that fit with her belief that computers could be creative? Read on and see if you can unscramble the paradox.

Ada was a mathematician with a creative flair and while Charles had come up with the innovative idea of the Analytical Engine itself, he didn’t see beyond his original idea of the computer as a calculator, she saw that they could do much more than that.

The key innovation behind her idea was that the numbers could stand for more than just quantities in calculations. They could represent anything – music for example. Today when we talk of things being digital – digital music, digital cameras, digital television, all we really mean is that a song, a picture, a film can all be stored as long strings of numbers. All we need is to agree a code of what the numbers mean – a note, a colour, a line. Once that is decided we can write computer programs to manipulate them, to store them, to transmit them over networks. Out of that idea comes the whole of our digital world.

Ada saw even further though. She combined maths with a creative flair and so she realised that not only could they store and play music they could also potentially create it – they could be composers. She foresaw the whole idea of machines being creative. She wasn’t just the first programmer, she was the first truly creative programmer.

– Paul Curzon, Queen Mary University of London

This article was originally published at the CS4FN website, along with other articles about Ada Lovelace. We also have a special Ada Lovelace-themed issue of the CS4FN magazine which you can download as a PDF (click picture below).

See also: The very first computers and Ada Lovelace Day (2nd Tuesday of October). Help yourself to our Women in Computing posters PDF.

 

The very first computers

Victorian engineer Charles Babbage designed, though never built the first mechanical computer. The first computers had actually existed for a long time before he had his idea, though. The British superiority at sea and ultimately the Empire was already dependent on them. They were used to calculate books of numbers that British sailors relied on to navigate the globe. The original meaning of the word computer was actually a person who did these calculations. The first computers were humans.

Globe with continents in binary
Image by Gordon Johnson from Pixabay (colour by CS4FN)

Babbage became interested in the idea of creating a mechanical computer in part because of computing work he did himself, calculating accurate versions of numbers needed for a special book: ‘The Nautical Almanac’. It was a book of astronomical tables, the result of an idea of Astronomer Royal, Nevil Maskelyne. It was the earliest way ships had to reliably work out their longitudinal (i.e., east-west) position at sea. Without them, to cross the Atlantic, you just set off and kept going until you hit land, just as Columbus did. The Nautical Almanac gave a way to work out how far west you were all the time.

Maskelyne’s idea was based on the fact that the angle from the moon’ to a person on the Earth and back to a star was the same at the same time wherever that person was looking from (as long as they could see both the star and moon at once). This angle was called the lunar distance.

The lunar distance could be used to work out where you were because as time passed its value changed but in a predictable way based on Newton’s Laws of motion applied to the planets. For a given place, Greenwich say, you could calculate what that lunar distance would be for different stars at any time in the future. This is essentially what the Almanac recorded.

Now the time changes as you move East or West: Dawn gradually arrives later the further west you go, for example, as the Earth rotates the sun comes into view at different times round the planet). That is why we have different time zones. The time in the USA is hours behind that in Britain which itself is behind that in China. Now suppose you know your local time, which you can check regularly from the position of the sun or moon, and you know the lunar distance. You can look up in the Almanac the time in Greenwich that the lunar distance occurs and that gives you the current time in Greenwich. The greater the difference that time is to your local time, the further West (or East) you are. It is because Greenwich was used as the fixed point for working the lunar distances out, that we now use Greenwich Mean Time as UK time. The time in Greenwich was the one that mattered!

This was all wonderful. Sailors just had to take astronomical readings, do some fairly simple calculations and a look up in the Almanac to work out where they were. However, there was a big snag. it relied on all those numbers in the tables having been accurately calculated in advance. That took some serious computing power. Maskelyne therefore employed teams of human ‘computers’ across the country, paying them to do the calculations for him. These men and women were the first industrial computers.

Before pocket calculators were invented in the 1970s the easiest way to do calculations whether big multiplication, division, powers or square roots was to use logarithms. The logarithm of a number is just the number of times you can divide it by 10 before you get to 1. Complicated calculations can be turned in to simple ones using logarithms. Therefore the equivalent of the pocket calculator was a book containing a table of logarithms. Log tables were the basis of all other calculations including maritime ones. Babbage himself became a human computer, doing calculations for the Nautical Almanac. He calculated the most accurate book of log tables then available for the British Admiralty.

The mechanical computer came about because Babbage was also interested in finding the most profitable ways to mechanise work in factories. He realised a machine could do more than weave cloth but might also do calculations. More to the point such a machine would be able to do them with a guaranteed accuracy, unlike people. He therefore spent his life designing and then trying to build such a machine. It was a revolutionary idea and while his design worked, the level of precision engineering needed was beyond what could be done. It was another hundred years before the first electronic computer was invented – again to replace human computers working in the national interest…but this time at Bletchley Park doing the calculations needed to crack the German military codes and so win the World War II.

More on …

Related Magazines …

Cover of Issue 20 of CS4FN, celebrating Ada Lovelace

EPSRC supports this blog through research grant EP/W033615/1.