Welcome to Day 3 of the CS4FN Christmas Computing Advent Calendar. The picture on the ‘box’ was a woolly bobble / pom-pom hat, so let’s see if we can find something computer-ish that might vaguely relate to that in a fairly tenuous way 🙂
Red woolly bobble hat with a white pom-pom on top. Very festive. Image drawn and digitised by Jo Brodie.
Keeping your (computer) cool
Hats help keep your head warm on a chilly day, keeping the warmth IN but computers need to have a way of keeping excess heat OUT to prevent damage to the components (…which are the things creating the heat in the first place of course). You don’t want to fry your graphics card or the Central Processing Unit (the CPU which is your computer’s brain).
I’m your biggest fan
Most computers have a fan which helps regulate the temperature and there are other design features that help heat flow away, including heat sinks which are designed so that a large surface area (which lets heat radiate away) can fit into a small area (see examples below).
Computer fan image by fancycrave1 from Pixabay showing black fan blades (just below the green, yellow and blue wires attached to the blue Intel sticker) above the grey metallic heat sink.
Above: three different types of heat sink, from Wikipedia. From left to right, pin fin, straight fin and flared heat sink designs. Image has been released into the public domain (CC0) by the photographer (‘Dtc5341’).
Cooling fluids
A much rarer way to remove heat from a computer has been to use a special coolant liquid. In 1985 the Cray-2 supercomputer (which was the fastest computer at the time) was cooled by being immersed in a cooling fluid called Fluorinert which, somewhat ironically, had a very high Global Warming Potential (very similar to the fluorocarbons that were once used to cool fridges).
A Cray-2 supercomputer. Cray 2, serial number 2013 with Static RAM [SRAM] and water fall style heat exchanger/reservoir. Photograph is in the public domain (CC0), created by NASA. Via Wikimedia Commons.
Reducing power
Another way of keeping computers cooled is to reduce their power so that they generate less heat in the first place. A modern computer in danger of overheating can run its processors and chips at a lower speed.
Bubble Sort
If you want to re-order a bobble hat you can just buy a new one but if you want to re-order lots of bobble hats (that is, put them in a particular order) you might use bobble sort, sorry – bubble sort, to re-order them by size or colour etc.
Bubble sort is an algorithm that lets you work your way through a list of items, comparing any two items and deciding which one goes before the other. You keep going through your list repeatedly until all the items are in the correct order. Computer scientists use lots of different ways to sort information but you can see the bubble sort danced out in the video below.
Computer memory molecular style, memristors, maths puzzle answer and a “20 questions” activity
Remember remember the 24th of December – as that’s the day to hang out your Christmas stocking! We’re halfway through our CS4FN Christmas Computing Advent Calendar and that’s the picture for today’s door. I’ve made the somewhat stretched link between a stocking as a store for your presents and computer memory as a store for all your data.
A Christmas stocking. No presents though. Yet… Image drawn and digitised by Jo Brodie.
If your own memory needs a prod you can find a list of our previous posts at the end of this one.
What happens when computers need so much memory that they start to test the laws of physics? Charlie Tizzard investigates.
A new way to store data in individual molecules might put some life back into an old law of computing. Back in 1965, the founder of Intel, Gordon Moore, noticed that computer chips doubled their performance about every 18 months. Not only was he right in 1965, he kept on being right. Ten, twenty, even thirty years later, chip power still doubled every 18 months. This observation was so strong that it began to seem like a law of nature. It was named “Moore’s law” after Gordon Moore himself.
But some experts believe that Moore’s law is beginning to waver. As electronics continue to get smaller and smaller they are pushing the law to the limit. Electronics are now so small that even the laws of physics are even getting in the way. An esteemed physicist, Michio Kaku, said that “we already see a slowing down of Moore’s law. Computing power simply cannot maintain its rapid exponential rise using standard silicon technology.” What to do?
Unless we move away from silicon-based storage in computing, we will run into some serious issues in the near future. Fortunately, scientists and engineers are experimenting with alternative ways of storing data. One way is to use molecules whose atoms can be shifted around within them. Storing data is all about making physical changes to something. That means you can put information in molecules by representing it as different atomic states. Best of all, those states can be changed and read by the same technology we have today: changes to the amount of electricity the molecules conduct.
Our only problem is that this idea works great inside a lab setting, but it can be difficult in the real world. First of all, molecular storage needs to be mass produced, but so far it’s specialised equipment built only in labs. Not only that, but up until now the molecules had to be kept at almost absolute zero (that’s -273°C) in order to work. But now an international team of researchers at MIT led by Jagadeesh Moodera have pioneered a new technique that allows the molecules to be kept at roughly the freezing point of water. In physics that’s practically room temperature.
ven more importantly, the molecules, which previously had to be sandwiched between two electrical conductors, only require one conductor in the MIT setup. That will make mass manufacturing a lot simpler and cheaper for companies. “This is only the tip of tip of the iceberg” says Moodera, so don’t be surprised if you are using chemicals for storing your photos in the future!
A memristor – photo from Wikimedia Commons. A memristor computer memory device that is enabled by an atomically-thin layer of coal-derived carbon manufactured by NETL. This work is in the public domain (CC0), created by the United States Department of Energy.
Electronics! It’s all been done long ago, hasn’t it? Resistors, transistors, capacitors, and inductors: all invented. See. Done it, filled in the worksheet, nothing else to discover…but did you miss the birth of the memristor?
In 2008 a new member of the electronics family was born. It had been discussed in theory as the missing link. It was mathematically possible, but never actually built till electronic engineers at Hewlett Packard used nanotechnology to bring it into existence.
Memristors are resistors with memory. Doh! Clever name! It can work as a data store, being either off or on, but it can store this information without any power too. This ability to store binary data (1s and 0s) with no drain on a battery, combined with its tiny, nanotechnology size means that memristors can store more data than any normal hard drive, and can be accessed as quickly as RAM – the kind of memory computers currently use. That means that in the future computers may be able to store more, start faster and be eco friendly too.
Building brains? That would be amazing enough but it turns out that the memistor has another trick up its nano-sleeve. Rather than working in digital mode, saving on/off (1,0) data like normal computer components, it can also hold values in between! The values it holds change every time the memristor receives an electrical signal, which is exactly what happens in the neurones of our brain as we learn. In the future networks of memristors could mimic the way our brains work, storing the things they learned from their electronic experiences. That would open up the possibility of a compact, low power way to build artificial intelligences.
Not bad for a humble little addition to the family of electronic components. See what you can miss is you don’t pay attention!
2. Today’s activity – the 20 questions game
The game 20 Questions, as the name suggests, involves trying to guess which famous person someone is thinking about by asking a maximum of 20 questions, all of which can be answered by YES or NO. The trick – of course – is to use good questions.
You’d be there all day if you kept asking them “Is it this person?”, “Is it that person?”. Those types of questions don’t chip away at the enormity of ~8 billion or so possibilities. Better questions might include “Are they alive?”, “Are they European?”. A yes or no answer to those questions tells you much more and helps narrow things down.
The game is a great way to learn about information theory and how the best questions are ones that split the options in half (roughly!). Most of the 8 billion people on Earth aren’t that famous, let’s assume it’s around 1 million people (because the maths is handy if we do!). If each of your questions divides a population of famous people in half each time and we start with one million people, how many questions do you need to ask before you get down to one person?
Or, to put it another way 2 (dividing in half) to the power of 20 (the 20 questions) or 220 gives 1,048,576 people (or items).
A correctly filled in answer for the kakuro puzzle. Image by Paul Curzon / CS4FN.
The creation of this post was funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.
A mathematical proof and a maths puzzle (but no hard sums, promise).
Thank you to everyone who’s been reading our Advent Calendar and said nice things about it and shared it with others. If you’re new to our pages you can see all our previous posts at the end.
We’re doing a post every day from the 1 – 25 December, loosely connected (if we can manage it!) to the theme suggested by the picture on the CS4FN Christmas Computing Advent Calendar.
Today’s picture on the Advent Calendar door is a Christmas pudding. Thanks to the phrase “the proof of the pudding is in the eating” (which I think means you have to eat all the chocolate puddings to know if they’re any good) I have chosen to match this picture with one of the CS4FN articles from the archives that is all about PROOF. Sadly we don’t seem to have any articles about pudding.
People sometimes pour brandy on Christmas puddings and set fire to it but this one has been iced instead and is not a fire hazard. Image drawn and digitised by Jo Brodie.
Graphic news images often help sway public opinion. Images of famine in Africa led to LiveAid, a massive relief effort in 1985. Images from war zones of civilians can be disturbing enough that war leaders lose or gain political support as a result (depending on who did the bad stuff). Images can have far more power than words to argue a case … to persuade.
Mathematical proofs are just arguments intended to persuade too. They aim to leave no element of doubt that some fact is true, not for emotional reasons but by logic. Mathematicians use mathematical notation – special symbols used in precise ways – to represent things in their proofs. That’s just a way of making sure the arguments are precise, with no room for doubt. Sometimes that can make them seem arcane and difficult to follow, though that’s only until you’ve learnt the mathematical language being used.
Mathematical proofs don’t have to use words and symbols though. In fact people have been presenting proofs as pictures at least since the Ancient Greeks, and just as with news images a diagrammatic proof can be much more persuasive. Sometimes just by looking at a diagram the truth of a fact can become obvious.
For example, here is a mathematical ‘fact’ we might want to prove:
“The square of any number is equal to the sum of consecutive odd numbers.”
That may sound a bit hairy. To get even hairier (if you aren’t a mathematician), we can write this precisely in mathematical notation as:
n2 = 1 + 3 + 5 + …+ (2n – 1)
Don’t worry about the notation though. Just look at the picture below. It shows what we mean by the fact and should persuade you it’s true.
The square of a number can be drawn as a picture of dots in a square. In other words one way to work out 102, say, is to create a square of dots with sides of length 10 and then count the dots. That’s why it’s called ‘squaring’!
A graphical representation of squaring numbers. Image by Paul Curzon / CS4FN.
One way to draw the dots to make up a square is as follows. First draw one dot in the corner, then draw three dots in an L-shape round it, then draw 5 dots in an L-shape round that…and keep going. Add a new L-shape (including the first dot) 10 times, say, once for each dot along the side, and you get a square of size 10 with 100 dots altogether. Notice that at every step you still have a square, though. Also notice that each L-shape is 2 bigger than the one before. That’s because you can make it by adding one dot on the end of each arm of the last L-shape.
That means the number of dots in a square can be calculated by adding a sequence of odd numbers, one for each L-shape added: 1 + 3 + 5 + … As you add L-shapes you work up through squares of all sizes, so all squares can be made by adding odd numbers in this way.
We’ve just explained it in words, but actually it’s all in the picture, so it’s possible to see without needing the words at all.
At least it may be possible for a person to see perhaps, but what about a computer? Could a computer ‘see’ a proof from a diagram? Computers are now very good at helping humans do logical proof using mathematical notation – after all they work themselves by pushing ‘symbols’ about and following rules blindly, which is all logical proof is. Seeing a proof in a diagram is different altogether though…or is it?
Mateja Jamnik, of the University of Cambridge has been tackling this problem. In fact her system, DIAMOND, can already check diagrammatic proofs created by a person to see if they really do convince. With DIAMOND you could, for example, take a series of L shape pictures like ours above and build them up step-by-step giving squares of different sizes. The system can then pull out the structure of this step-by-step proof and from that automatically obtain the equation that it proves.
DIAMOND needs a person to develop a diagrammatic proof for it to check. In the future, if Mateja has her way, the computers will be devising new diagrammatic proofs themselves that then convince we humans.
2. Today’s puzzle – Logic and Proof FUNdamentals
(This text, by Paul Curzon, was originally published over several pages at the CS4FN website)
It is often said that being good at Maths is important for Computer Scientists. So what’s the link? Well a lot of the more obviously fun sides of maths are actually computer science too, like how to do puzzles such as Rubik’s Cubes, puzzles about weird and wonderful characters crossing rivers, how to win at strategy games, and doing Sudoku. The Maths you do in solving a Sudoku is the same kind of reasoning as that behind getting computer programs to work.
It is not so much the actual Maths you learn at school that is important. It is more that a similar way of thinking is important: logical reasoning. Doing Maths at school is one good way to start to learn how to think that way. So if you are good at Maths you will probably be good at Computer Science, though (using a bit of logical reasoning) that doesn’t mean the opposite follows of course.
Kakuro, Logic and Computer Science
To be a good computer scientist you have to enjoy problem solving. That is what it’s all about: working out the best way to do things. You also have to be able to think in a logical way: be a bit of a Vulcan. But what does that mean? It just means being able to think precisely, extracting all the knowledge possible from a situation just by pure reasoning. It’s about being able to say what is definitely the case given what is already known…and it’s fun to do. That’s why there is a Sudoku craze going on as I write. Sudoku are just pure logical thinking puzzles. Personally I like Kakuro better. They are similar to Sudoku, but with a crossword format.
What is a Kakuro?
A Kakuro is a crossword-like grid, but where each square has to be filled in with a digit from 1-9 not a letter. Each horizontal or vertical block of digits must add up to the number given to the left or above, respectively. All the digits in each such block must be different. That part is similar to Sudoku, though unlike Sudoku, numbers can be repeated on a line as long as they are in different blocks. Also, unlike Sudoku, you aren’t given any starting numbers, just a blank grid.
Where does logic come into it? Take the following fragment:
There is a horizontal block of two cells that must add up to 16. Ways that could be done using digits 1-9 are 9+7, 8+8 or 7+9. But it can’t be 8+8 as that needs two 8s in a block which is not allowed so we are left with just two possibilities: 9+7 or 7+9. Now look at the vertical blocks. One of them consists of two cells that add up to 17. That can only be 9+8 or 8+9. That doesn’t seem to have got us very far as we still don’t know any numbers for sure. But now think about the top corner. We know from across that it is definitely 9 or 7 and from down that it is definitely 9 or 8. That means it must be 9 as that is the only way to satisfy both restrictions.
Kakuro image above by Paul Curzon / CS4FN.
A Kakuro for you to try
Here is a full Kakuro to try. The answer will be in tomorrow’s post.
Being able to think logically is important because computer programming is about coming up with precise solutions that even a computer can follow. To do that you have to make sure all the possibilities have been covered. Reasoning very much like in a Kakuro is needed to convince yourself and others that a program does do what it is supposed to.
Conjure up a stereotypical image of a scientist and they likely will have a white coat. If not brandishing test tubes, you might imagine them working with mice scurrying around a maze. In future the scientists may well be doing a lot of programming, and the mice for their part will be scurrying around in their own virtual world wearing Virtual Reality goggles.
Scientists have long used mazes as away to test the intelligence of mice, to the point it has entered popular culture as a stereotypical thing that scientists in white lab coats do. Mazes do give ways to test intelligence of animals, including exploring their memory and decision making ability in controlled experiments. That can ultimately help us better understand how our brains work too, and give us a better understanding of intelligence. The more we understand animal cognition as well as human cognition, the more computer scientists can use that improved understanding to create more intelligent machines. It can also help neurobiologists find ways to improve our intelligence too.
Flowers for Algernon is a brilliant short story and later novel based on the idea, there using experiments on mice and humans to test surgery intended to improve intelligence. In a slightly different take on mice-maze experiments, Douglas Adams, in ‘The Hitchhikers Guide to the Galaxy’, famously claimed that the mice were actually pan-dimensional beings and these experiments were really incredibly subtle experiments the mice were performing on humans. Whatever the truth of who is experimenting on who, the experiments just took a great leap forward because scientists at Northwestern University have created Virtual Reality goggles for their mice.
For a long time researchers at Northwestern have used a virtual reality version of maze experiments, with mice running on treadmills with screens around them projecting what the researchers want them to see, whether mazes, predators or prey. This has the advantage of being much easier to control than using physical mazes, and as the mice are actually stationary the whole time , just running on a treadmill, brain-scanning technology can be used to see what is actually happening in their brains while facing these virtual trials. The problem though is that the mice, with their 180 degree vision, can still see beyond the edges of the screens. The screens also give no sense of 3 dimensions, when like us the mice naturally see in 3D. As the screens are not fully immersive, they are not fully natural and that could affect the behaviour of the mice and so invalidate the experimental results.
That is why the Northwestern researchers invented the mousey VR googles, the idea being that they would give a way to totally immerse the mice in their online world, and so improve the reliability of the experiments. In the current version the goggles are not actually worn by the mice, as they are still too heavy. Instead, the mouse’s head is held in place really close to them, but with the same effect of total immersion. Future versions may be small enough for the mice to wear them though.
The scientists have already found that the mice react more quickly to events, like the sight of a predator, than in the old set-up, suggesting that being able to see they were in a lab was affecting their behaviour. Better still, there are new kinds of experiment that can be done with this set up. In particular, the researchers have run experiments where an aerial predator like an owl appears from above the mice in a natural way. Mounting screens above them previously wasn’t possible as it got in the way of the brain scanning equipment. What does happen when a virtual owl appears? The mice either run faster or freeze, just as in the wild. This means that by scanning their brains while this is happening, how their perception of the threat works can be investigated, as well as how decision-making is taking place at the level of their brain activity. The scientists also intend to run similar experiments where the mouse is the predator, for example chasing a virtual fly too. Again this would not have been possible previously.
That in any case is what we think the purpose of these new experiments is. What new and infinitely subtle experiments it is allowing the pan-dimensional mice to perform on us remains to be seen.
Chatbots, knowing where your files are, and winning at noughts and crosses with artificial intelligence.
Welcome to Day 10 of our CS4FN Christmas Computing Advent Calendar. We are just under halfway through our 25 days of posts, one every day between now and Christmas. You can see all our previous posts in the panel with the Christmas tree at the end.
Today’s picture-theme is Holly (and ivy). Let’s see how I manage to link that to computer science 🙂
Sprig of holly. Image drawn and digitised by Jo Brodie.
1. Holly – or Alexa or Siri
In the comedy TV series* Red Dwarf the spaceship has ‘Holly’ an intelligent computer who talks to the crew and answers their questions. Star Trek also has ‘Computer’ who can have quite technical conversations and give reports on the health of the ship and crew.
People are now quite familiar with talking to computers, or at least giving them commands. You might have heard of Alexa (Amazon) or Siri (Apple / iPhone) and you might even have talked to one of these virtual assistants yourself.
When this article (below) was written people were much less familiar with them. How can they know all the answers to people’s questions and why do they seem to have an intelligence?
Read the article and then play a game (see 3. Today’s Puzzle) to see if you think a piece of paper can be intelligent.
Meet the Chatterbots – talking to computers thanks to artificial intelligence and virtual assistants
*also a book!
2. Are you a filing cabinet or a laundry basket?
People have different ways of saving information on their computers. Some university teachers found that when they asked their students to open a file from a particular directory their students were completely puzzled. It turned out that the (younger) students didn’t think about files and where to put them in the same way that their (older) teachers did, and the reason is partly the type of device teachers and students grew up with.
Older people grew up using computers where the best way to organise things was to save a file in a particular folder to make it easy to find it again. Sometimes there would be several folders. For example you might have a main folder for Homework, then a year folder for 2021, then folders inside for each month. In the December folder you’d put your december.doc file. The file has a file name (december.doc) and an ‘address’ (Homework/2021/December/). Pretty similar to the link to this blog post which also uses the / symbol to separate all the posts made in 2021, then December, then today.
Files and folders image by Ulrike Mai from Pixabay. Each brown folder contains files, and is itself contained in the drawer, and the drawer is contained in the cabinet.
To find your december.doc file again you’d just open each folder by following that path: first Homework, then 2021, then December – and there’s your file. It’s a bit like looking for a pair of socks in your house – first you need to open your front door and go into your home, then open your bedroom door, then open the sock drawer and there are your socks.
What your file and folder structure might look like. Image created by Jo Brodie for CS4FN.
Younger people have grown up with devices that make it easy to search for any file. It doesn’t really matter where the file is so people used to these devices have never really needed to think about a file’s location. People can search for the file by name, by some words that are in the file, or the date range for when it was created, even the type of file. So many options.
The first way, that the teachers were using, is like a filing cabinet in an office, with documents neatly packed away in folders within folders. The second way is a bit more like a laundry basket where your socks might be all over the house but you can easily find the pair you want by typing ‘blue socks’ into the search bar.
Which way do you use?
In most cases either is fine and you can just choose whichever way of searching or finding their files that works for you. If you’re learning programming though it can be really helpful to know a bit about file paths because the code you’re creating might need to know exactly where a file is, so that it can read from it. So now some university teachers on STEM (science, technology, engineering and maths) and computing courses are also teaching their students how to use the filing cabinet method. It could be useful for them in their future careers.
As the author says “Many consumer devices try to conceal the underlying file system from the user (for example, smart phones and some tablet computers). Graphical interfaces, applications, and even search have all made it possible for people to use these devices without being concerned with file systems. When you study Computer Science, you must look behind these interfaces.”
You might be wondering what any of this has to do with ivy. Well, whenever I’ve seen a real folder structure on a Windows computer (you can see one here) I’ve often thought it looked a bit like ivy 😉
Creeping ivy at Blackheath station in London. Photographed by Jo Brodie for CS4FN.
Print or write out the instructions on page 5 of the PDF and challenge someone to a game of noughts and crosses… (there’s a good chance the bit of paper will win).
The trick is based on a very old puzzle at least one early version of which was by Sam Lloyd. See this selection of vanishing puzzles for some variations. A very simple version of it appears in the Moscow Puzzles (puzzle 305) by Boris A. Kordemsky where a line is made to disappear.
Images drawn by Jo Brodie for CS4FN.
In the picture above five medium-length lines become four longer lines. It looks like a line has disappeared but its length has just been spread among the other lines, lengthening them.
If you’d like to have a go at drawing your own disappearing puzzle have a look here.
Computing- and food-themed post on cookies and spam + a puzzle.
Welcome to Day 9 of our CS4FN Christmas Computing Advent Calendar. Every day between now and Christmas we’ll publish a post about computer science with a puzzle to print and solve. You can see all our previous posts in the list at the end.
Today’s post is inspired by the picture on the advent calendar’s door – a gingerbread man, so we have a food-themed post. Well… food-ish.
Festive gingerbread man. Image drawn and digitised by Jo Brodie.
1. Cookies, but not the biscuit kind
Imagine you have a Christmas gift voucher and want to spend it in an online shop. You visit the website and see an item you’d like so you click ‘add to basket’ and then look for some other things you’d like to buy. You click on another item to find out more about it but suddenly your basket is empty! Fortunately this doesn’t usually happen thanks to cookies, which are tiny computer files that can make your website visit run smoothly.
Websites ask you if they can put these cookies on your computer. If you say ‘yes’ that lets them see that you are the same person as you add new things to your basket. It would be no use if you added your second item and the website decided that you were now a completely different person. Some cookies help the organisation know that you’re still you, even when you’re viewing lots of different pages on their website.
Other cookies mean that you don’t have to keep logging in every time you click on a new page within the website. It would be very annoying if you had to do that.
Some cookies are there to help the organisation itself. They let them see what people are clicking on when they’re on the organisation’s website, and what path they follow as they visit different pages. They can also tell what device someone is using (a phone or a computer) so they can make sure the information is set to be the right size on their screen.
If people are logged in then the website knows who they are. Because of this, organisations have to be very careful about how they use this information, to protect their visitors’ privacy. If they don’t take care then they are breaking the law and can be fined a lot of money.
Further reading
Cookies (no publication date given) – from the ICO – the Information Commissioner’s Office.
2. The recipe for spam
These days when people talk about “spam” they are talking about unwanted emails from strangers. The word spam comes from a tinned meat product which, because of a comedy sketch by Monty Python, now also means “email messages that no-one can avoid”.
Shutting down spammers is tough for the authorities, so the internet’s arteries go on getting plugged up by spam. The best strategy against it so far seems to be filtering out junk emails from your inbox. Lots of early spam filtering relied on keeping lists of words that appear in spam and catching emails that contained them, but there were plenty of problems. For one thing, certain words that turn up in spam also appear sometimes in normal emails, so perfectly innocent messages sometimes ended up in the spam filter. What’s more, spammers have ways of eluding filters that simply check words against a list. Just me55 a-r-0-u-n-d w1th teh sp£lling.
Finally a simple but ingenious idea surfaced: instead of trying to keep a list of spammy words, why not try and teach computers to recognise spam for themselves? There’s a whole branch of maths about probability that researchers began to apply to spam, and a programmer called Paul Graham made the strategy famous in 2002 when he wrote an essay called A Plan for Spam.
Spammy maths
Paul Graham suggested that you could analyse the words you get in a sample of your email to see what the chances are that a particular word would appear in your real messages. You could do the same with a sample from your spam. Then you could look up any word in a new message and see whether it’s likely to be spam or your real email.
Of course, one word’s not enough to base your conclusion on, so Paul’s filter chose the fifteen most interesting words to look at. What that meant was that it grabbed the biggest clues to look at – words that, statistically, had the best chance of being in either spam or real mail, but not both. Then it used those clues to figure out the overall chance that an email is spam. It did this with an equation called Bayes’ theorem, which tells you how to figure out the chances of something being true given a set of facts. In this case Bayes’ theorem figures out the chances of a message being spam given the set of words in it.
What’s brilliant about the statistical approach is that not only does the computer learn as it goes on, meaning it keeps up with spammers’ tricks automatically, it can learn what words are normal for each person’s email, so scientists working on Viagra wouldn’t have to worry about all their emails going in the bin.
On guard online
Spam filters now work well enough that you can make your inbox pretty safe from the porky hordes of messages trying to invade. Wonderful news for the 99% of us who don’t have any use for dodgy meds, fake fashions and pyramid scams. As long as people keep buying into spam and the small group of overlords keeps turning computers into zombies, we’ll need to keep our defences up.
3. Today’s puzzle – the melting snowman
A picture showing several snowmen, drawn by Paul Curzon.
Instructions
One of the snowmen keeps disappearing! Is it melting or just flying away, and which one is it?
Cut out the picture along the straight black lines, to give three rectangular pieces. Then follow the simple algorithm and see the snowman disappear before your eyes.
1. Put the three pieces together in the original positions to make the picture. 2. Count all the snowmen. 3. Swap the position of the top two pieces over so the top and bottom halves of the snowmen line up again 4. Count the snowmen again.
One snowman has disappeared!
Put the pieces back and you will find it reappears.
The explanation and answer will arrive in tomorrow’s (blog) post 🙂
Tim Berners-Lee, Right to Repair, and a maths puzzle.
Welcome to Day 8 of our CS4FN Christmas Computing Advent Calendar. It features a computing-themed post every day in December until Christmas Day. The blog posts in the Advent Calendar are inspired by the picture on the ‘door’ – and today’s post is inspired by a picture of a Christmas present.
Presents are something you give freely to someone, but they’re also something you hide behind wrapping paper. This post is about a gift and also about trying to uncover something that’s been hidden. Read on to find out about Tim Berners-Lee’s gift to the world, and about the Restart Project who are working to stop the manufacturers of electronic devices from hiding how people can fix them. At the bottom of the post you’ll find the answer to yesterday’s puzzle and a new puzzle for today, also all of the previous posts in this series. If you’re enjoying the posts, please share them with your friends 🙂
A present in blue wrapping paper with a large green bow. Image drawn and digitised by Jo Brodie.
1. “This is for everyone” – Tim Berner’s Lee
Audiences don’t usually cheer for computer scientists at major sporting events but there’s one computer scientist who was given a special welcome at the London Olympics Opening Ceremony in 2012.
Tim Berners-Lee invented the World Wide Web in 1989 by coming up with the way for web pages to be connected through links (everything that’s blue and clickable on this page is a link). That led to the creation of web browsers which let us read web pages and find our way around them by clicking on those links. If you’ve ever wondered what “www” means at the start of a link it’s just short for World Wide Web. Try saying “www” and then “World Wide Web” – which takes longer to say?
Tim Berners-Lee didn’t make lots of money from his invention. Instead he made the World Wide Web freely available for everyone to use so that they could access the information on the web. Unless someone has printed this onto paper, you’re reading this on a web browser on the World Wide Web, so three cheers Tim Berners-Lee.
In 2004 the Queen knighted him (he’s now Sir Tim Berners-Lee) and in 2017 he was given a special award, named after Alan Turing, for “inventing the World Wide Web and the first web browser.”
Below is the tweet he sent out during the Olympics opening ceremony.
You might also like finding out about “open-source software” which is “computer software that is released under a license in which the copyright holder grants users the rights to use, study, change, and distribute the software and its source code to anyone and for any purpose.”
2. Do you have the right to repair your electronic devices?
A ‘black box’ is a phrase to describe something that has an input and an output but where ‘the bit in the middle’ is a complete mystery and hidden from view. An awful lot of modern devices are like this. In the past you might have been able to mend something technological (even if it was just changing the battery) but for devices like mobile phones it’s becoming almost impossible.
People need special tools just to open them as well as the skills to know how to open them without breaking some incredibly important tiny bit. Manufacturers aren’t always very keen for customers to fix things. The manufacturers can make more money from us if they have to sell us expensive parts and charge us for people to fix them. Some even put software in their devices that stops people from fixing them!
The cost of fixing devices can be very expensive and in some cases it can actually be cheaper to just buy a new device. Obviously it’s very wasteful too.
The Restart Project is full of volunteers who want to help everyone fix our electronic devices, and also fix our relationship with electronics (discouraging us from throwing away our old phone when a new one is on the market). The project began in London but they now run Repair Parties in several cities in the UK and around the world. At these parties people can bring their broken devices and rather than just ‘getting them fixed’ they can learn how to fix their devices themselves by learning and sharing new skills. This means they save money and save their devices from landfill.
Restart have also campaigned for people to have the Right to Repair their own devices. They want a change in manufacturing laws to make sure that devices are designed so that the people who buy and use them can easily repair them without having to spend too much money.
A more mathematical puzzle today. Rather than writing letters into the kriss-kross you need to write the equation and its answer.
For example 5 + 2 = as the clue gives you 5 + 2 = 7 as the answer which takes up 5 characters (note that the answer is not “seven” which also takes up 5 characters!). There are several places in the puzzle where a 5 character answer could go, but which one is the right one? Start with the clues that have only one space they can fit into (the ones with 7 symbols and 9 symbols) then see what can fit around them.
This puzzle was created by Daniel, who was aged 6 when he made this. For an explanation of the links to computer science and how these puzzles can be used in the classroom please see the Maths Kriss-Kross page on our site for teachers. Note that the page does include the answer sheet, but no cheating, we’ll post the answer tomorrow. Also, if you don’t have a printer you can use the editable PDF linked on that page.
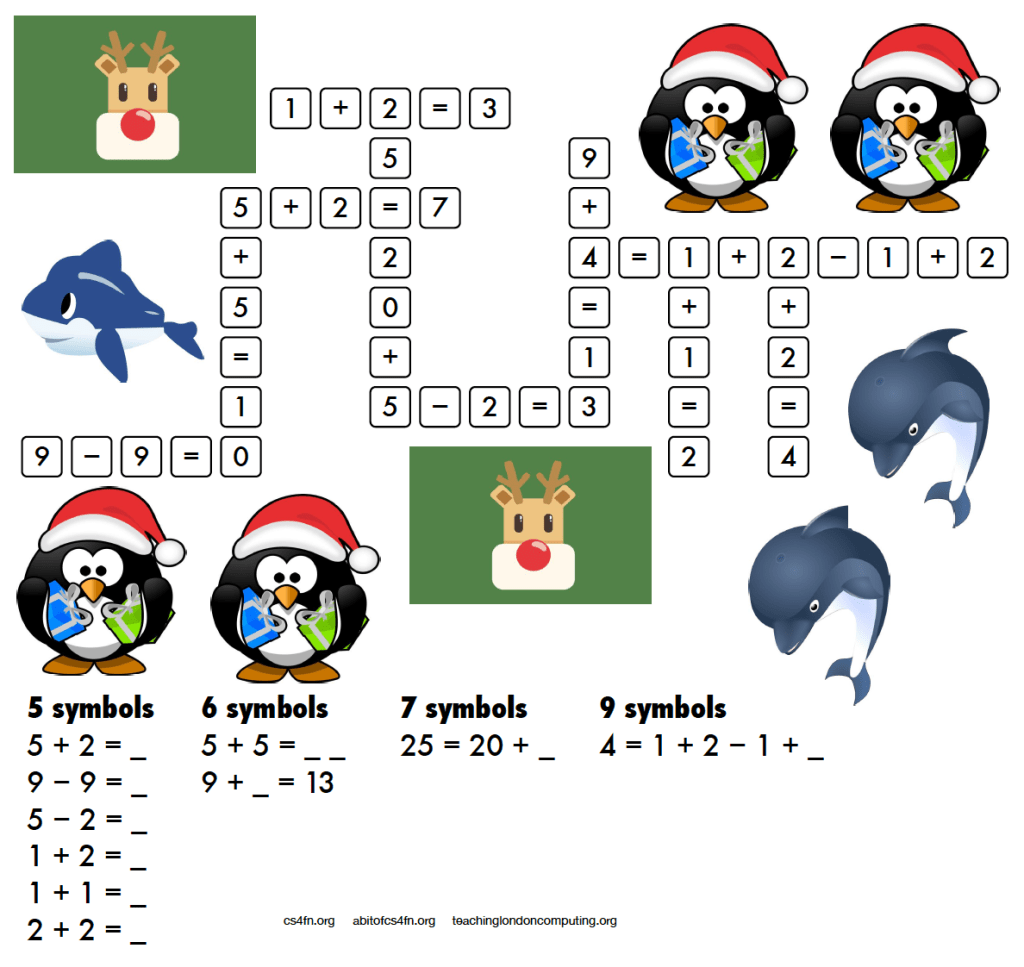
4. Answer to yesterday’s puzzle
The creation of this post was funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.
Welcome to Day 7 of our advent calendar. Yesterday’s post was about Printed Circuit Birds Boards, today’s theme is the Christmas robin redbreast which features on lots of Christmas cards and today is making a special appearance on our CS4FN Computing advent calendar.
A little robin redbreast. Image drawn and digitised by Jo Brodie.
In this longer post we’ll focus on the ways computer scientists are learning about our feathered friends and we’ll also make room for some of the bird-brained April Fools jokes in computing too.
We hope you enjoy it, and there’s also a puzzle at the end.
1. Computing Sounds Wild – bird is the word
Our free CS4FN magazine, Computing Sounds Wild (you can download a copy here), features the word ”bird” 60 times so it’s definitely very bird-themed.
“An interest in nature and an interest in computers don’t obviously go well together. For a band of computer scientists interested in sound they very much do, though. In this issue we explore the work of scientists and engineers using computers to understand, identify and recreate wild sounds, especially those of birds. We see how sophisticated algorithms that allow machines to learn, can help recognize birds even when they can’t be seen, so helping conservation efforts. We see how computer models help biologists understand animal behaviour, and we look at how electronic and computer-generated sounds, having changed music, are now set to change the soundscapes of films. Making electronic sounds is also a great, fun way to become a computer scientist and learn to program.”
2. Singing bird – a human choir singing birdsong
by Jane Waite, QMUL This article was originally published on the CS4FN website and can also be found on page 15 in the magazine linked above.
“I’m in a choir”. “Really, what do you sing?” “I did a blackbird last week, but I think I’m going to be woodpecker today, I do like a robin though!”
This is no joke! Marcus Coates a British artist, got up very early, and working with a wildlife sound recordist, Geoff Sample, he used 14 microphones to record the dawn chorus over lots of chilly mornings. They slowed the sounds down and matched up each species of bird with different types of human voices. Next they created a film of 19 people making bird song, each person sang a different bird, in their own habitats, a car, a shed even a lady in the bath! The 19 tracks are played together to make the dawn chorus. See it on YouTube below.
Marcus didn’t stop there, he wrote a new bird song score. Yes, for people to sing a new top ten bird hit, but they have to do it very slowly. People sing ‘bird’ about 20 times slower than birds sing ‘bird’ ‘whooooooop’, ‘whooooooop’, ‘tweeeeet’. For a special performance, a choir learned the new song, a new dawn chorus, they sang the slowed down version live, which was recorded, speeded back up and played to the audience, I was there! It was amazing! A human performance, became a minute of tweeting joy. Close your eyes and ‘whoop’ you were in the woods, at the crack of dawn!
Computationally thinking a performance
Computational thinking is at the heart of the way computer scientists solve problems. Marcus Coates, doesn’t claim to be a computer scientist, he is an artist who looks for ways to see how people are like other animals. But we can get an idea of what computational thinking is all about by looking at how he created his sounds. Firstly, he and wildlife sound recordist, Geoff Sample, had to focus on the individual bird sounds in the original recordings, ignore detail they didn’t need, doing abstraction, listening for each bird, working out what aspects of bird sound was important. They looked for patterns isolating each voice, sometimes the bird’s performance was messy and they could not hear particular species clearly, so they were constantly checking for quality. For each bird, they listened and listened until they found just the right ‘slow it down’ speed. Different birds needed different speeds for people to be able to mimic and different kinds of human voices suited each bird type: attention to detail mattered enormously. They had to check the results carefully, evaluating, making sure each really did sound like the appropriate bird and all fitted together into the Dawn Chorus soundscape. They also had to create a bird language, another abstraction, a score as track notes, and that is just an algorithm for making sounds!
3. Sophisticated songbird singing – how do they do it?
by Dan Stowell, QMUL This article was originally published on the CS4FN website and can also be found on page 14 in the magazine linked above.
How do songbirds make such complex sounds? The answer is on a different branch of the tree of evolution… We humans have a set of vocal folds (or vocal cords) in our throats, and they vibrate when we speak to make the pitched sound. Air from your lungs passes over them and they chop up the column of air letting more or less through and so making sound waves. This vocal ‘equipment’ is similar in mammals like monkeys and dogs, our evolutionary neighbours. But songbirds are not so similar to us. They make sounds too, but they evolved this skill separately, and so their ‘equipment’ is different: they actually have two sets of vocal folds, one for each lung.
Sometimes if you hear an impressive, complex sound from a bird, it’s because the bird is actually using the two sides of their voice-box together to make what seems like a single extra-long or extra-fancy sound. Songbirds also have very strong muscles in their throat that help them change the sound extremely quickly. Biologists believe that these skills evolved so that the birds could tell potential mates and rivals how healthy and skillful they were.
So if you ever wondered why you can’t quite sing like a blackbird, now you have a good excuse!
4. Data transmitted on the wing
Computers are great ways of moving data from one place to another and the internet can let you download or share a file very quickly. Before I had the internet at home if I wanted to work on a file on my home computer I had to save a copy from my work computer onto a memory stick and plug it in to my laptop at home. Once I ‘got connected’ at home I was then able to email myself with an attachment and use my home broadband to pick up file. Now I don’t even need to do that. I can save a file on my work computer, it synchronises with the ‘cloud’ and when I get home I can pick up where I left off. When I was using the memory stick my rate of data transfer was entirely down to the speed of road traffic as I sat on the bus on the way to work. Fairly slow, but the data definitely arrived in one piece.
In 1990 a joke memo was published for April Fool’s Day which suggested the use of homing pigeons as a form of internet, in which the birds might carry small packets of data. The memo, called ‘IP over Avian Carriers’ (that is, a bird-based internet), was written in a mock-serious tone (you can read it here) but although it was written for fun the idea has actually been used in real life too. Photographers in remote areas with minimal internet signal have used homing pigeons to send their pictures back.
The beautiful (and quite possibly wi-fi ready, with those antennas) Victoria Crowned Pigeon. Not a carrier pigeon admittedly, but much more photogenic. Image by Foto-Rabe from Pixabay
A company in the US which offers adventure holidays including rafting used homing pigeons to return rolls of films (before digital film took over) back to the company’s base. The guides and their guests would take loads of photos while having fun rafting on the river and the birds would speed the photos back to the base, where they could be developed, so that when the adventurous guests arrived later their photos were ready for them.
On April Fool’s Day in 2002 Google ‘admitted’ to its users that the reason their web search results appeared so quickly and were so accurate was because, rather than using automated processes to grab the best result, Google was actually using a bank of pigeons to select the best results. Millions of pigeons viewing web pages and pecking picking the best one for you when you type in your search question. Pretty unlikely, right?
In a rather surprising non-April Fool twist some researchers decided to test out how well pigeons can distinguish different types of information in hospital photographs. They trained pigeons by getting them to view medical pictures of tissue samples taken from healthy people as well as pictures taken from people who were ill. The pigeons had to peck one of two coloured buttons and in doing so learned which pictures were of healthy tissue and which were diseased. If they pecked the correct button they got an extra food reward.
The researchers then tested the pigeons with a fresh set of pictures, to see if they could apply their learning to pictures they’d not seen before. Incredibly the pigeons were pretty good at separating the pictures into healthy and unhealthy, with an 80 per cent hit rate.
You can download this as a PDF to PRINT or as an editable PDF that you can fill in on a COMPUTER.
You might wonder “What do these kriss-kross puzzles have to do with computing?” Well, you need to use a bit of logical thinking to fill one in and come up with a strategy. If there’s only one word of a particular length then it has to go in that space and can’t fit anywhere else. You’re then using pattern matching to decide which other words can fit in the spaces around it and which match the letters where they overlap. Younger children might just enjoy counting the letters and writing them out, or practising phonics or spelling.
We’ll post the answer tomorrow.
7. Answer to yesterday’s puzzle
Image by Paul Curzon / CS4FN.
The creation of this post was funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.
Welcome to Day 6 of the CS4FN Christmas Computing Advent Calendar – every day until Christmas we’ll post a little something about computer science. Some of it will even relate (…vaguely) to the picture on the advent calendar’s door.
Today’s picture is of a festive bauble with a pattern engraved on it. That obviously made us think of printed circuit boards. Read on to see why.
A brightly coloured (pink!) Christmas bauble, ready to go on a tree. Image drawn and digitised by Jo Brodie.
Printed Circuit Boards
Yesterday we looked at computers made of water, in which the flow of water (and where it ends up) let people do some quite advanced calculations. Today it’s the electrons that are doing the flowing… through tiny little copper channels.
This post is behind the 5th ‘door’ of the CS4FN Christmas Computing Advent Calendar – we’re publishing a computing-themed (and sometimes festive-themed) post every day until Christmas Day. Today’s picture is a snowman, and what’s a snowman made of but frozen water?
Image drawn and digitised by Jo Brodie.
1. You can make a computer out of water!
1n 1936 Vladimir Lukyanov got creative with some pipes and pumps built a computer, called a water (or hydraulic) integrator, which could store water temporarily in some bits and pump water to other bits. The movement of water and where it ended up used the ‘simplicity of programming’ to show him the answer – a physical representation of some Very Hard Sums (sums, equations and calculations that are easier now thanks to much faster computers).
A simple and effective way of using water to show a mathematical relationship popped up on QI and the video below demonstrates Pythagoras’ Theorem rather nicely.
Video from the BBC via their YouTube channel.
In 1939 Lukyanov published an article about his analog hydraulic computer for the (‘Otdeleniye Technicheskikh Nauk’ or ‘Отделение технических наук’ in Russian which means Section for Technical Scientific Works although these days we’d probably say Department of Engineering Sciences) and in 1955 this was translated by the Massachusetts Institute of Technology (MIT) for the US army’s “Arctic Construction and Frost Effects Laboratory”. You can see a copy of his translated ‘Hydraulic Apparatus for Engineering Computations‘ at the Internet Archive.
In a rather pleasing coincidence for this blog post (that you might think was by design rather than just good fortune) this device was actually put to work by the US Army to study the freezing and thawing not of snowmen but of soil (ie, the ground). It’s particularly useful if you’re building and maintaining a military airfield (or even just roads) to know how well the concrete runway will survive changes in weather (and how well your aircraft’s wheels will survive after meeting it).
For a modern take on the ‘hydrodynamic calculating machine’ aka water computer see this video from science communicator Steve Mould in which he creates a computer that can do some simple additions.
Video by Steve Mould via his YouTube channel.
2. The puzzle of digital compression
Our snowman’s been sitting around for a while and his ice has probably become a bit compacted, so he might be taking up less space (or he might have melted). Compression is a technique computer scientists use to make big data files smaller.
Big files take a long time to transfer from one place to another. The more data the longer it takes, and the more memory is needed to store the information. Compressing the files saves space. Data on computers is stored as long sequences of characters – ultimately as binary 1s and 0s. The idea with compression is that we use an algorithm to change the way the information is represented so that fewer characters are needed to store exactly the same information.
That involves using special codes. Each common word or phrase is replaced by a shorter sequence of symbols. A long file can be made much shorter if it has lots of similar sequences, just as the message below has been shortened. A second algorithm can then be used to get the original back. We’ve turned the idea into a puzzle that involves pattern matching patterns from the code book. Can you work out what the original message was? (Answer tomorrow, and another snowman-themed puzzle coming soon).
The code: NG1 AMH5 IBEC2 84F6JKO 7JDLC93 (clue: Spooky apparitions are about to appear on Christmas Eve).
The code book (match the letter or number to the word it codes for).
3. Answer to yesterday’s puzzle
The creation of this post was funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.
cs4fn 
