Category: LGBTQ+

How did the zebra get its stripes?

Head of a fish with a distinctive stripy, spotty pattern
Image by geraldrose from Pixabay

There are many myths and stories about how different animals gained their distinctive patterns. In 1901, Rudyard Kipling wrote a “Just So Story” about how the leopard got its spots, for example. The myths are older than that though, such as a story told by the San people of Namibia (and others) of how the zebra got its stripes – during a fight with a baboon as a result of staggering through the baboon’s fire. These are just stories. It was a legendary computer scientist and mathematician, who was also interested in biology and chemistry, who worked out the actual way it happens.

Alan Turing is one of the most important figures in Computer Science having made monumental contributions to the subject, including what is now called the Turing Machine (giving a model of what a computer might be before they existed) and the Turing Test (kick-starting the field of Artificial Intelligence). Towards the end of his life, in the 1950s, he also made a major contribution to Biology. He came up with a mechanism that he believed could explain the stripy and spotty patterns of animals. He has largely been proved right. As a result those patterns are now called Turing Patterns. It is now the inspiration for a whole area of mathematical biology.

How animals come to have different patterns has long been a mystery. All sorts of animals from fish to butterflies have them though. How do different zebra cells “know” they ultimately need to develop into either black ones or white ones, in a consistent way so that stripes (not spots or no pattern at all) result, whereas leopard cells “know” they must grow into a creature with spots. They both start from similar groups of uniform cells without stripes or spots. How do some that end up in one place “know” to turn black and others ending up in another place “know” to turn white in such a consistent way?

There must be some physical process going on that makes it happen so that as cells multiply, the right ones grow or release pigments in the right places to give the right pattern for that animal. If there was no such process, animals would either have uniform colours or totally random patterns.

Mathematicians have always been interested in patterns. It is what maths is actually all about. And Alan Turing was a mathematician. However, he was a mathematician interested in computation, and he realised the stripy, spotty problem could be thought of as a computational kind of problem. Now we use computers to simulate all sorts or real phenomena, from the weather to how the universe formed, and in doing so we are thinking in the same kind of way. In doing this, we are turning a real, physical process into a virtual, computational one underpinned by maths. If the simulation gets it right then this gives evidence that our understanding of the process is accurate. This way of thinking has given us a whole new way to do science, as well as of thinking more generally (so a new kind of philosophy) and it starts with Alan Turing.

Back to stripes and spots. Turing realised it might all be explained by Chemistry and the processes that resulted from it. Thinking computationally he saw that you would get different patterns from the way chemicals react as they spread out (diffuse). He then worked out the mathematical equations that described those processes and suggested how computers could be used to explore the ideas.

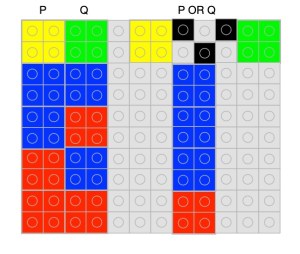
Diffusion is just a way by which chemicals spread out. Imagine dropping some black ink onto some blotting paper. It starts as a drop in the middle, but gradually the black spreads out in an increasing circle until there is not enough to spread further. The expanding circle stops. Now, suppose that instead of just ink we have a chemical (let’s call it BLACK, after its colour), that as it spreads it also creates more of itself. Now, BLACK will gradually uniformly spread out everywhere. So far, so expected. You would not expect spots or stripes to appear!

Next, however, let’s consider what Turing thought about. What happens if that chemical BLACK produces another chemical WHITE as well as more BLACK? Now, starting with a drop of BLACK, as it spreads out, it creates both more BLACK to spread further, but also WHITE chemicals as well. Gradually they both spread. If the chemicals don’t interact then you would end up with BLACK and WHITE mixed everywhere in a uniform way leading to a uniform greyness. Again no spots or stripes. Having patterns appear still seems to be a mystery.

However, suppose instead that the presence of the WHITE chemical actually stops BLACK creating more of itself in that region. Anywhere WHITE becomes concentrated gets to stays WHITE. If WHITE spreads (ie diffuses) faster than BLACK then it spreads to places first that become WHITE with BLACK suppressed there. However, no new BLACK leads to no more new WHITE to spread further. Where there is already BLACK, however, it continue to create more BLACK leading to areas that become solid BLACK. Over time they spread around and beyond the white areas that stopped spreading and also create new WHITE that again spreads faster. The result is a pattern. What kind of pattern depends on the speed of the chemical reactions and how quickly each chemical diffuses, but where those are the same because it is the same chemicals the same kind of pattern will result: zebras will end up with stripes and leopards with spots.

This is now called a Turing pattern and the process is called a reaction-diffusion system. It gives a way that patterns can emerge from uniformity. It doesn’t just apply to chemicals spreading but to cells multiplying and creating different proteins. Detailed studies have shown it is the mechanism in play in a variety of animals that leads to their patterns. It also, as Alan Turing suggested, provides a basis to explain the way the different shapes of animals develop despite starting from identical cells. This is called morphogenesis. Reaction-diffusion systems have also been suggested as the mechanism behind how other things occur in the natural world, such as how fingerprints develop. Despite being ignored for decades, Turing’s theory now provides a foundation for the idea of mathematical biology. It has spawned a whole new discipline within biology, showing how maths and computation can support our understanding of the natural world. Not something that the writers of all those myths and stories ever managed.

– Paul Curzon, Queen Mary University of London

More on …

Magazines …

Front cover of CS4FN issue 29 - Diversity in Computing

Subscribe to be notified whenever we publish a new post to the CS4FN blog.

This page is funded by EPSRC on research agreement EP/W033615/1.

QMUL CS4FN EPSRC logos

The logic behind syntactic sugar

Computer Scientists talk about “Syntactic Sugar” when talking about programming languages. But in what way might a program be made sweet? It is all about how necessary a feature of a language is, and the idea and phrase was invented by Computer Scientist and gay activist, Peter Landin. He realised it made it easier to define the meaning of languages in logic and made the definitions more elegant.

Raspberry on a spoon full of sugar with sugar cascading around
Image by Myriams-Fotos from Pixabay

Peter Landin was involved in the development of several early and influential programming languages but also a pioneer of the use of logic to define exactly what each construct of a programming language did: the language’s “semantics”.  He realised there was a fundamental difference between different parts of a language. Some were absolutely fundamental to the language. If you removed them then programs would have to be written in a different way, if at all, as a result. Remove the assignment construct that allows a program to change the value of variables, for example, and there are things your programs can no longer do, or at least it would need to do it in very different way. Remove the feature that allows someone to write i++ instead of i = i + 1, on the other hand, and nothing much changes about how you write code. They were just abbreviations for common uses of the more core things. 

As another example, suppose you didn’t like using curly brackets to start and end blocks of code (perhaps having learnt to program using Pascal) then if programming in C or Java you could add a layer of syntactic sugar by replacing { by BEGIN and } by END. Your programs might look different and make you feel happier, but were not really any different.

Peter called these kinds of abbreviations “syntactic sugar”. They were superficial, just there to make the syntax (the way things were written at the level of spelling and punctuation)  a little bit nicer for the programmers: sometimes more readable, sometimes just needing less typing.

It is now recognised, of course, that writing readable code is a critically important part of programming. Code has to be maintainable: easily understood and modified by others long after it was written. Well thought out syntactic sugar can help with this as well as making it easier to avoid mistakes when writing code in the first place. For example, syntactic sugar is used in many languages to give special syntax to core datatypes, where they are called sugared types. Common example include using quotes to represent a String value like “abc” or square brackets like [1,2,3] to stand for an array value, rather than writing out the underpinning function calls of the core language to construct a value.

People now sometimes deride the idea of syntactic sugar, but it had a clear use for Peter beyond just readability. He was interested in logically defining languages: saying in logic exactly what each construct meant. The syntactic sugar distinction made his life doing that easier. The fundamental things were the things that he had to define directly in logic. He had to work out exactly what the semantics of each was and how to say what they meant mathematically. Syntactic sugar could be defined just by adding rewrite rules that convert the syntactic sugar to the core syntax. i++, for example does not need to be defined logically, just converted to  i = i + 1 to give its meaning. If assignment was defined in terms of logic then the abbreviation is ultimately too as a result.

Peter discussed this in relation to treating a kind of logic called the lambda calculus as the basis for a language. Lambda Calculus is a logic based on functions. Everything consists of lambda expressions, though he was looking at a version which included arithmetic too. For example, in this logic, the expression:

(λn.2+n)

defines a function that takes a value n and returns the value resulting from adding 2 to that value. Then the expression:

(λn.2+n) [5]

applies that function to the value 5, meaning 5 is substituted for the n that comes after the lambda, so it simplifies to 2+5 or further to 7. Lambda expressions, therefore, have a direct equivalence to function call in a programming language. The lambda calculus has a very simple and precise mathematical meaning too, in that any expression is just simplified by substituting values for variables as we did to get the answer 7 above. It could be used as a programming language in itself. Logicians (and theoretical computer scientists) are perfectly happy reading lambda calculus statements with λ’s, but Peter realised that as a programming language it would be unreadable to non-logicians. However with a simple change, adding syntactic sugaring, it could be made much more readable. This just involved replacing the Greek letter λ by the word “where” and altering the order and throwing in an = sign..

Now instead of writing

(λn.2+n) [5]

in his programming language you would write

2 + n where n = 5

Similarly,

(λn.3n+2) [a+1]

became

3n+2 where n = a + 1

This made the language much more readable but did not complicate the task of defining the semantics. It is still just directly equivalent to the lambda calculus so the lambda calculus can still be used to define its semantics in a simple way (just apply those transformations backwards). Overall this work showed that the group of languages called functional programming languages could be defined in terms of lambda calculus in a very elegant way.

Syntactic sugar is at one level a fairly trivial idea. However, in introducing it in the context of defining the semantics of languages it is very powerful. Take the idea to its extreme and you define a very small and elegant core to your language in logic. Then everything else is treated as syntactic sugar with minimal work to define it as rewrite rules. That makes a big difference in the ease of defining a programming language as well as encouraging simplicity in the design. It was just one of the ways that Peter Landin added elegance to Computer Science.

by Paul Curzon, Queen Mary University of London

More on …

Magazines …

Our Books …

Subscribe to be notified whenever we publish a new post to the CS4FN blog.

EPSRC supports this blog through research grant EP/W033615/1. 

Peter Landin: Elegance from Logic

Celebrating LGBTQ+ Greats

Thousands of programming languages have been invented in the many decades since the first. But what makes a good language? A key idea behind language design is that they should make it easy to write complex algorithms in simple and elegant ways. It turns out that logic is key to that. Through his work on programming language design, Peter Landin as much as anyone, promoted both elegance and the linked importance of logic in programming. 

Pride flag with lambda x.x (identity) superimposed
Pride image by Image by Pete Linforth from Pixabay. Composite by PC

Peter was an eminent Computer Scientist who made major contributions to the theory of programming languages and especially their link to logic. However, he also made his mark in his stand against war, and support of the nascent LGBTQ+ community in the 1970s as a member of the Gay Liberation Front. He helped reinvigorate the annual Gay Pride marches as a result of turning his house into a gay commune where plans were made. It’s as a result of his activism as much as his computer science that an archive of his papers has been created in the Oxford Bodleian Library.

However, his impact on computer science was massive. He was part of a group of computing pioneers aiming to make programming computers easier, and in particular to move away from each manufacturer having a special programming language to program their machines. That approach meant that programs had to be rewritten to work on each different machine, which was a ridiculous waste of effort! Peter’s original contribution to programming languages was as part of the team who developed the programming language, ALGOL which most modern programming languages owe a debt to.

ALGOL included the idea of recursion, allowing a programmer to write procedures and functions that call themselves. This is a very mathematically elegant way to code repetition in an algorithm (the code of the function is executed each time it calls itself). You can get an idea of what recursion is about by standing between two mirrors. You see repeated versions of your reflection, each one smaller than the last. Recursion does that with problem solving. To solve a problem convert it to a similar but smaller version of the same problem (the first reflection). How do you solve that smaller problem? In the same way, as a smaller version of the same problem (the second reflection)… You keep solving those similar but smaller problems in the same way until eventually the problem is small enough to be trivial and so solved. For example, you can program a factorial method (multiplying all numbers from 1 to n together),in this way. You write that to compute factorial of a number, n, it just calls itself and computes the factorial of (n-1). It just multiply that result by n to get the answer. In addition you just need a trivial case eg that factorial of 1 is just 1.

factorial (1) = 1
factorial (n) = n * factorial (n-1)

Peter was an enthusiastic and inspirational teacher and taught ALGOL to others. This included teaching one of the other, then young but soon to be great, pioneers of Programming Theory, Tony Hoare. Learning about recursion led Hoare to work out a way, using recursion, to finally explain the idea that made his name in a simple and elegant way: the fast sorting algorithm he invented called Quicksort. The ideas included in ALGOL had started to prove their worth.

The idea of including recursion in a programming language was part of the foundation for the idea of functional programming languages. They are mathematically pure languages that use recursion as the way to repeat instructions. The mathematical purity makes them much easier to understand and so write correct programs in. Peter ran with the idea of programming in this way. He showed the power that could be derived from the fact that it was closely linked to a kind of logic called the Lambda Calculus, invented by Alonso Church. The Lambda Calculus is a logic built around  mathematical functions. One way to think about it is that it is a very simple and pure way to describe in logic what it means to be a mathematical function – as something that takes arguments and does computation on them to give results. This Church showed was a way to define all possible computation just as Turing’s Turing machine is. It provides a simple way to express anything that can be computed.

Peter showed that the Lambda Calculus could be used as a way to define programming languages: to define their “semantics” (and so make the meaning of any program precise).

Having such a precise definition or “semantics” meant that once a program was written it would be sure to behave the same way whatever actual computer it ran on. This was a massive step forward. To make a new programming language useful you had to write compilers for it: translators that convert a program written in the language to a low level one that runs on a specific machine. Programming languages were generally defined by the compiler up till then and it was the compiler that determined what a program did. If you were writing a compiler for a new machine you had to make sure it matched what the original compiler did in all situations … which is very hard to do.

So having a formal semantics, a mathematical description of what a compiler should do, really makes a difference. It means anyone developing a new compiler for a different machines can ensure the compiler matches that semantics. Ultimately, all compilers behave the same way and so one program running on two different manufacturer’s machines are guaranteed to behave the same way in all situations too.

Peter went on to invent the programming language ISWIM to illustrate some of his ideas about the way to design and define a programming language. ISWIM stands for “If you See What I Mean”. A key contribution of ISWIM was that the meaning of the language was precisely defined in logic following his theoretical work. The joke of the name meant it was logic that showed what he meant, very precisely! ISWIM allowed for recursive functions, but also allowed recursion in the definition of data structures. For example, a List is built from a List with a new node on the end. A Tree is built from two trees forming the left and right branches of a new node. They are defined in terms of themselves so are recursive.

Building on his ideas around functional programming, Peter also invented something he called the SECD machine (named after its components: a Stack, Environment, Control and Dump). It effectively implements the Lambda calculus itself as though it is a programming language.ISWIM provided a very simple but useful general-purpose low level language. It opened up a much easier way to write compilers for functional programming languages for different machines. Just one program needed to be written that compiled the language into SECD. Then you had a much simpler job of writing a compiler to convert from the low level SECD language to the low level assembly language of each actual computer.  Even better, once written, that low level SECD compiler could be used for different functional programming languages on a single machine. In SECD, Peter also solved a flaw in ALGOL that prevented functions being fully treated as data. Functions as Data is a powerful feature of the best modern programming languages. It was the SECD design that first provided a solution. It provided a mechanism that allowed languages to pass functions as arguments and return them as results just as you could do with any other kind of data without problem.

In the later part of his life Peter focussed much more on his work supporting the LGBTQ+ community having decided that Computer Science was not doing the good for humanity he once hoped. Instead, he thought it was just supporting companies making profit, ahead of the welfare of people. He decided that he could do more good as part of the LGBTQ+ community. Since his death there has been an acceleration in the massing of wealth by technology companies, whereas support for diversity has made a massive difference for good, so in that he was prescient. His contributions have certainly, though, provided a foundation for better software, that has changed the way we live in many ways for the better. Because of his work they are less likely to cause harm because of programming mistakes, for example, so in that at least he has done a great deal of good.

by Paul Curzon, Queen Mary University of London

More on …

Magazines …

Our Books …

Subscribe to be notified whenever we publish a new post to the CS4FN blog.

EPSRC supports this blog through research grant EP/W033615/1. 

Mary Ann Horton and the invention of email attachments

by Paul Curzon, Queen Mary University of London

A glowing envelope flying over a grid of envelopes
Image by Divya Gupta from Pixabay

Mary Ann Horton was transitioning to female at the time that she made one of her biggest contributions to our lives with a simple computer science idea with a big impact: a program that allowed binary email attachments.

Now we take the idea of sending each other multimedia files – images, video, sound clips, programs, etc for granted, whether by email or social networks, Back in the 1970s, before even the web had been invented, people were able to communicate by email, but it was all text. Email programs worked on the basis that people were just sending words, or more specifically streams of characters, to each other. An email message was just a long sequence of characters sent over the Internet. Everything in computers is coded as binary: 1s and 0s, but text has a special representation. Each character has its own code of 1s and 0s, that can also be thought of as a binary number, but that can be displayed as the character by programs that process it. Today, computers use a universally accepted code called Unicode, but originally most adopted a standard code called ASCII. All these codes are just allocations of patterns of 1s and 0s to each character. In ASCII, ‘a’ is represented by 1100001 or the number 97, whereas A is 1000001 or number 65, for example. These are only 7 bits long and as computers store data in bytes of 8 bits at a time this means that not all patterns of binary (so representable numbers) correspond to one of the displayable characters that email messages were expected to contain by the programs that processed them.

That is fine if all you have done is used programs like text editors, that output characters so you are guaranteed to be sending printable characters. The problem was other kinds of data whether images or runnable programs, are not stored as sequences of characters. They are more general binary files, meaning the data is long sequences of byte-sized patterns of 1s and 0s and what those 1s and 0s meant depended on the kind of data and representation used. If email programs were given such data to send, pass on or receive, they would reject or more likely mangle it as not corresponding to characters they could display. The files didn’t even have to be non-character formats, as at the time some computer systems used a completely different code for characters. This meant text emails could also be mangled just because they passed through a computer using a different format of character.

Mary Ann realised that this was all too restrictive for what people would be needing computers to do. Email needed to be more flexible. However, she saw that there was a really easy solution. She wrote a program, called uuencode that could take any binary file and convert it to one that was slightly longer but contained only characters. A second program she wrote, called uudecode converted these files of characters back to the original binary file to be saved by the receiving email program exactly it was originally on the source program.

All the uuencode program did was take 3 bytes (24 bits) of the binary file at a time, split them into groups of 6 bits so effectively representing a number from 0 to 63, add 32 to this number so the numbers are now in the range 32 to 95 and those are the numbers so binary patterns of the printable characters that the email programs expected. Each three bytes were now 4 printable characters. These could be added to the text of an email, though with a special start and end sequence included to identify it as something to decode. uudecode just did this conversion backwards, turning each group of 4 characters back into the orginal three bytes of binary.

Email attachments had been born, and ever since communication programs, whether email, chat or social media, have allowed binary files, so multimedia, to be shared in similar ways. By seeing a coming problem, inventing a simple way to solve it and then writing the programs, Mary Ann Horton had made computers far more flexible and useful.

More on …

Related Magazines …

cs4fn issue 14 cover

Subscribe to be notified whenever we publish a new post to the CS4FN blog.

This blog is funded through EPSRC grant EP/W033615/1.

The first computer wizard

by Paul Curzon, Queen Mary University of London

A rainbow coloured checkers board
Image by CS4FN

Christopher Strachey did a series of firsts in computer programming, and that was just when he was playing.

With father a cryptographer, mother a suffragist, Christopher Strachey was a school teacher when he first started ‘playing’ with computers in the early 1950s. He had been given the chance to write programs, first for the National Physical Laboratories’ ACE computer and then the Manchester Mark 1: two of the earliest working computers in the world. The range of things he achieved is amazing. He probably created the first serious computer game you could play against (a draughts playing game), the first recorded computer music, the first “creative” program (a love letter writing program) … and he was just enjoying himself.

He went on to do serious computing, becoming an early computer consultant and later led the Oxford University Programming Research Group. He invented the idea of time-sharing computers, developed the CPL language (the ancestor of C and so many modern programming languages, so has had a powerful effect on all subsequent programming language design). Perhaps most notably, with Dana Scott he pioneered the idea of using maths to describe the meaning of programming languages, called denotational semantics. Oh, and he was a wizard debugger too, famous for quickly debugging his own and other people’s programs. He achieved all of this despite poor performance at school and university when younger, and despite suffering a nervous breakdown when at university that interrupted his studies. It has been suggested that the breakdown might have been due to him coming to terms with the fact that he was homosexual: now legal, homosexuality was then illegal in the UK.

More on …

Related Magazines …

This blog is funded by UKRI, through grant EP/W033615/1.

Edie Schlain Windsor and same sex marriage

CS4FN Banner
US Supreme court building Image by Mark Thomas from Pixabay
Image by Mark Thomas from Pixabay

Edie Schlain Windsor was a senior systems programmer at IBM. There is more to life than computing though. Just like anyone else, Computer Scientists can do massively important things aside from being very good at computing. Civil rights and over-turning unjust laws are as important as anything. She led the landmark Supreme Court Case (United States versus Windsor) that was a milestone for the rights of same-sex couples in the US.

Born to a Jewish immigrant family, Edie worked her way up from an early data entry job at New York University to ultimately become a senior programmer at IBM and then President of her own software consultancy where she helped LGBTQ+ organisations become computerised.

Having already worked as a programmer at an energy company called Combustion Engineering, she joined IBM on completing her degree in 1958 so was one of the early generation of female programmers, before the later idea of the male programmer stereotype took hold. Within ten years she had been promoted to the highest technical position in IBM, that of a Senior Systems Programmer: so one of their top programmers lauded as a wizard debugger. She had started out programming mainframe computers, the room size computers that were IBM ‘s core business at the time. They both designed and built the computers as well as the operating system and other software that ran on them. Edie became an operating systems expert, and a pioneer computer scientist also working on natural language processing programs, aiming to improve the interactivity of computes. Natural Language Processing was then a nascent area but that by 2011 IBM led spectacularly with its program Watson winning the quiz show Jeopardy! answering general knowledge questions playing against human champions.

Before her Supreme Court case overturned it, a law introduced in 1996 banned US federal recognition of same-sex marriages. It made it federal law that marriage could only exist between a man and a woman. Individual states in the US had introduced same-sex marriage but this new law meant that such marriages were not recognised in general in the US. Importantly, for those involved it meant a whole raft of benefits including tax, immigration and healthcare benefits that came with marriage were denied to same-sex couples.

Edie had fallen in love with psychologist Thea Spyer in 1965, and two years later they became engaged, but actually getting married was still illegal. They had to wait almost 30 years before they were even allowed to make their partnership legal, though still at that point not marry. They were the 80th couple to register on the day such partnerships were finally allowed. By this time Thea had been diagnosed with multiple sclerosis, a disease that gradually leads to the central nervous system breaking down, with movement becoming ever harder. Edie was looking after her as a full time carer, having given up her career to do so. They both loved dancing and did so throughout their life together even once Thea was struggling to walk, using sticks to get on to the dance floor and later dancing in a wheelchair. As Thea’s condition grew worse it became clear she had little time to live. Marriage was still illegal in New York, however, so before it was too late, they travelled to Canada and married there instead.

When Thea died she left everything to Edie in her will. Had Edie been a man married to Thea, she would not have been required to pay tax on this inheritance, but as a woman and because same-sex marriages were deemed illegal she was handed a tax bill of hundreds of thousands of dollars. She sued the government claiming the way different couples were treated was unfair. The case went all the way to the highest court, the Supreme Court, who ruled that the 1996 law was itself unlawful. Laws in the US have as foundation a written constitution that dates back to 1789. The creation of the constitution was a key part of the founding of the United States of America itself. Without it, the union could easily have fallen apart, and as such is the ultimate law of the land that new laws cannot overturn. The problem with the law banning same sex marriage was that it broke the 5th amendment of the constitution added in 1791, one of several amendments made to ensure people’s rights and justice was protected by the constitution.

The Supreme Court decision was far more seismic than just refunding a tax bill, however. It overturned the law that actively banned same-sex marriage, as it fell foul of the constitution, and this paved the way for such marriages to be made actively legal. In 2014 federal employees were finally told they should perform same-sex marriages across the US, and those marriages gave the couple all the same rights as mixed-sex marriages. Because Edie took on the government, the US constitution, and so justice for many, many couples prevailed.

– Paul Curzon, Queen Mary University of London

More on …

Related Magazines …

cs4fn issue 14 cover

This blog is funded through EPSRC grant EP/W033615/1.

Lego Computer Science: Logic with Truth Tables

Lego of a truth table for NOT P
The truth table for NOT P. A yellow brick represents P. Blue means True and Red means false. Read along the rows to get the meaning of NOT P when P is true or false. Image by CS4FN

We have seen how to represent truth tables in lego. Truth tables are a way of giving precise meaning to logical operations like AND, OR and NOT. They are also give a way to do logical reasoning following a simple algorithm.

That’s Not Not True

You may have been pulled up in English and told you just said the opposite of what you meant, after saying something like “There ain’t no way I’m doing that”. This is a “double negative” as the “n’t” in “ain’t” is really “not” so followed by “no way” you are actually saying “not not way” or overall: “I am doing that”. Perhaps the most famous double negative is in the Rolling Stones song “(I can’t get no) satisfaction”. English is very flexible though and double negatives like this don’t cancel out but just become a different way of saying the negative version. In logic two negations do cancel out, though. Let’s take a purer version to work with: the statement “I am not not happy”. What does this mean? In logic the basic proposition here is “I am not happy”. The logical statement is “NOT (NOT (I am happy))”.

We can prove what this means using truth tables. We can do more than just prove what this single statement means. We can prove what all double negatives mean, more generally. We do this by replacing the proposition “I am happy” with a variable P. It now becomes NOT (NOT P) or in our lego version where we use a yellow brick to mean a proposition, P:

NOT NOT P
Image by CS4FN

This is just syntax, just a sequence of symbols. It doesn’t give us any meaning on its own. We can build truth tables in Lego for that. We start from the variables that are at the inside of the logical expression which here is just the variable P. We list in a table column the possible values it can take (true or false).

Image by CS4FN

This shows P (yellow) can be either be TRUE (blue) or FALSE (red). Now we build up the logical expression of interest a column at a time. NOT is applied to P, so we add a new column for NOT P and use the truth table for the operator, NOT, to tell us what lego brick to put in each row based on the lego brick already there. The NOT truth table is at the top of the page. It says if you have a blue brick in a row, place a red brick there. If you have a red brick, put a blue brick there. This gives us a new filled out column for (NOT P) which is just a copy of the NOT truth table (but bare with us that was just a simple case). We get:

Image by CS4FN

Moving outwards in the expression NOT (NOT P)), we now look at the operator applied to (NOT P). It is NOT again. We add a new column to our truth table and again use the NOT truth table to work out the new values, but this time applied to the column before (the NOT P column). The NOT truth table says put a blue brick for a red brick, and a red brick for a blue brick in the column it is being applied to (the NOT P column). This gives:

NOT (NOT P) lego truth table
Image by CS4FN

The result is a truth table with coloured bricks identical to that of the original column for P. Switching back from lego bricks to what the columns mean, we have shown that the NOT(NOT P) column is the same as the P column, or in other words that NOT(NOT P) EQUALS P (whatever value P has).

We can actually go a step further though, because equivalence is just a logical operation with its own truth table. It gives true if the two operands have the same value and false otherwise (or in lego terms if the bricks are the same colour the answer is a blue brick and if they are different colours the answer is a red brick. The truth table looks like this:

P EQULAS Q lego truth table
Image by CS4FN

We can use this truth table to calculate whether two lego truth table columns are equal or not just by looking up the combinations in this EQUALS truth table. Continuing our example we can carrying building our truth table about NOT(NOT P)). To make things clearer first add a column corresponding to P again. That means we will be applying the EQUALS operator to the last two columns. As before, for each row, look up the corresponding pattern for those last two columns in the EQUALS truth table to get the answer for that row. In the first row we have two blue bricks so that becomes a blue brick according tot he EQUALS truth table. In the next row we have two red bricks. That also becomes a blue brick. This gives:

Lego truth table for NOT (NOT P) EQUALS P
Image by CS4FN

The thing to notice here is that all the entries in the final answer column are blue lego pieces. Switching back from the lego world to the logic world, what does this mean? Blue is true so all rows in the answer are true. That means whatever value of the proposition P the answer to NOT (NOT P) EQUALS P is true. We have proved a theorem that this is always true. We have shown by building with lego that a double negation cancels itself out.

Logical expressions like this that are always true (whatever the values of the variables) are called tautologies. We can tell something is a tautology, so we have proved a theorem, just by the simple manual check that its truth table values are true (or in lego all blue).

The important thing to realise about this is all the reasoning can be done without knowing what the symbols mean, and certainly not worrying about English words, once you have the truth tables. You do it mechanically. You do not need to think about what, for example, red and blue mean until the end. At that point you return to the logical world to see what you have found out. All blue means it is always true! You can also at that point substitute back in actual words of interest into the statements proved. P means “I am happy”. We started by asking what “I am not not happy” means. We converted this to “NOT (NOT (I am happy))”. By swapping in “I am happy” for P in our theorem gives us that NOT (NOT “I am happy”) EQUALS “I am happy”, or that “I am not not happy.” just means the same as “I am happy”

We have been reasoning about English statements, but this kind of reasoning is the basis of all logical reasoning and essentially the basis of formal verification where the meaning of programs and hardware is checked to see if it meets a specification. It tells you what a test in a program like “if (! temperature != 0) …) means so does for example, or what a circuit with two NOT gates does.

And lego logic has even given us a way to prove things just by building with lego.

– Paul Curzon, Queen Mary University of London

More on …

Lego Computer Science

Image shows a Lego minifigure character wearing an overall and hard hat looking at a circuit board, representing Lego Computing
Image by Michael Schwarzenberger from Pixabay

Part of a series featuring featuring pixel puzzles,
compression algorithms, number representation,
gray code, binary, logic and computation.

EPSRC supports this blog through research grant EP/W033615/1, The Lego Computer Science post was originally funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.

Lego Computer Science: Truth Tables

Lego of a truth table for NOT P

Truth tables are a simple way of reason about logic that were popularised by the 20th century philosopher Ludwig Wittgenstein. They provide a very clear way to explain what logical operators like AND, OR and NOT mean (or in computational terms, what they do). They also give a simple way to do pure logical reasoning and so see if arguments follow logically. These logical operators crop up in logic circuits and in programs where decisions are being made so are vital to creating correct circuits and writing correct programs. Let’s see what a truth table is by making some from Lego.

Logic in Lego

First we need to represent the basic building blocks of logic in lego. We’ve seen in previous articles how to represent numbers, binary and even images in lego. We have seen that we do computation on symbols and we can use lego blocks as symbols. Logic can therefore be represented in lego symbols too.

We will look at a simple kind of logic called propositional logic (there isn’t actually just one kind of logic but lots of different kinds with different rules). Propositional logic is the simplest kind. It deals with propositions which are just statements that are either true or false (but we may not know which). For example, “Snoopy is a logician.” is a proposition. So are “The world is flat.”, “Water contains oxygen.” and “temperature > 0” as we might find in a program. For the purposes of logic itself, it doesn’t matter what the words actually mean or even what they are. We will therefore represent all propositions by square lego blocks of different colours.

Here we want the symbols to stand for logical things rather than numbers. There are lots of numerical values: things like 1, 5 and 77. There are only two logical values: TRUE and FALSE, often written just as T and F. We will use a blue lego block for the logical value TRUE, and a red block for the value FALSE. They are just symbols though so we could use any blocks and any colours, just as we could use other words for true and false as other languages do. We chose blue for true just because it rhymes so is easy to remember, and red more randomly because it is a common lego primary colour.

True and False lego. A square 2x2 blue block is True. A square 2x2 red block is false.
True and False lego. A square 2×2 blue block represents True. A square 2×2 red block is false.

What about representing the actual sentences stating purported facts like “Messi is the best footballer ever”, or in a program “n == 1”? Statements like this are called propositions. As far as reasoning logically goes the precise words or even language they are in do not matter. This is something Wittgenstein realised. When doing reasoning these basic propositions can be replaced by variables like P and Q and the logic won’t change. Rather than use letters we will just use different coloured lego blocks to stand for different propositions, emphasising that the words or even variable names do not matter. So we will use a yellow block for a variable P and a green block for a variable Q. Each of which could stand for absolutely any English proposition we like at any time (though if we want it to stand for a particular proposition then we should define which one clearly).

Yellow block for P and green block for Q
Propositional variables P and Q are represented by yellow and green blocks

Logical Symbols

What we are really interested in is not just true and false values but the logical operations on propositions. The core of these we use in everyday English: AND, OR and NOT, more technically known as conjunction, disjunction and negation in logic. There are several variations of the symbols used to represent these symbols just as there are for true and false. We will use the versions in lego as below.

Symbols for AND, OR and NOT in Lego
The logical operators AND, OR and NOT as lego symbols

These lego symbols will allow us to write out logical expressions about propositions: like “The cat is thirsty AND NOT the cat is hungry” which we might write in English as “The cat is thirsty and not hungry”. If we use a yellow block to mean “The cat is thirsty” and a green block to mean “The cat is hungry” then in lego logic we can write it as follows:

P AND (NOT Q) in Lego symbols
The cat is thirsty AND NOT the cat is hungry
P AND (NOT Q)

Of course the yellow and green brick are variables so by changing the propositions they represent it can stand for other things. It can also represent: ” The moon is blue AND NOT The moon is made of cheese.” where the yellow brick represents “The moon is blue” and the green brick represents “The moon is made of cheese”.

Think up some statements that involve AND, OR and NOT and then build representations of then in lego logic like the above.

The meaning of logical connectives

The above gives us symbols for the logical connectives, but so far they have no meaning: it is just syntax. Perhaps you think you know what the words mean. We use words like and, or and not in language rather imprecisely at times based on dictionary-style definitions. They essentially mean the same in English as in logic, but we need to define what they mean precisely. We do not want two different people to have two slightly different understandings of what they mean. This is where truth tables come in. A truth table tells us exactly, and without doubt, what the symbols for the operators mean. The give what is called by computer scientists a formal semantics to the logical connectives.

Let’s look at NOT first. A truth table is just a table that includes as rows all the combinations of true and false values of the variables in a logical expression together with an answer for those values. For example a truth table for the operator NOT, so telling us in all situations what (NOT a) means, is:

PNOT P
TRUEFALSE
FALSETRUE
A truth table for the NOT operator. Reading along the rows,
IF P is TRUE THEN (NOT P) is FALSE;
IF P is FALSE THEN (NOT P) is TRUE.

We can build this truth table in lego using our lego representation:

Lego of a truth table for NOT P

NOT only applies to one proposition, the one it negates, (it is a unary logical connective). That means we only need two rows in the table to cover the different possible values those propositions could stand for. AND (and OR) combine to two propositions (it is a binary logical connective). To cover all the possible combinations of the values of those propositions we need a table with four rows as there are four possibilities.

PQ P AND Q
TRUETRUETRUE
TRUEFALSEFALSE
FALSETRUEFALSE
FALSEFALSEFALSE
A truth table for the logical AND operator.

We can build this in Lego as:

Lego of a truth table for P AND Q

Reading along the rows this says that if both P and Q are blue (true) then the answer for P AND Q is true. Otherwise the answer is false (red). T

The following is the lego truth table for the logical OR operator

Lego of a truth table for P AND Q

The columns for the two variables yellow/green (P/Q) are the same, setting out all the possibilities. Now the answer is true (blue) if either operand is true (blue) and false (red) when both are false (red).

We have now created lego truth tables that give the meaning of each of these three logical connectives. They aren’t the only logical operators – in fact there are 8 possible binary ones. Have a go at building lego truth tables for other binary logical connectives such as exclusive-or which is true if exactly one of the operands is true, and equivalence which is true if both operands are the same truth value.

Truth tables give precise meanings to logical operators and so to logic. That is useful, but even more usefully, they give a way to reason logically in a clear, price way. By following a simple algorithm to build new truth tables from existing ones, we can prove general facts, that are ultimately about propositions, in lego… as we will see next.

– Paul Curzon, Queen Mary University of London

Lego Computer Science

Image shows a Lego minifigure character wearing an overall and hard hat looking at a circuit board, representing Lego Computing
Image by Michael Schwarzenberger from Pixabay

Part of a series featuring featuring pixel puzzles,
compression algorithms, number representation,
gray code, binary and computation.

More on …

EPSRC supports this blog through research grant EP/W033615/1, The Lego Computer Science post was originally funded by UKRI, through grant EP/K040251/2 held by Professor Ursula Martin, and forms part of a broader project on the development and impact of computing.

Ludwig Wittgenstein: tautology and truth tables

A jigsaw of the word truth with pieces missing Image by Gerd Altmann from Pixabay
Image by Gerd Altmann from Pixabay

Ludwig Wittgenstein is one of the most important philosophers of the 20th century. His interest was in logic and truth, language, meaning and ethics. As an aside he made contributions to logical thinking that are a foundation of computing. He popularised truth tables, a way to evaluate logical expressions, and invented the modern idea of tautology. His life shows that you do not have to set out with your life planned out to ultimately do great things.

Wittgenstein was born in Austria, of three-quarters Jewish descent, and actually went to the same school as Hitler at the same time, as they were the same age to within a week. Had he still been in Austria at the time of World War II he would undoubtedly have been sent to a concentration camp. Hitler presumably would not have thought much of him had he known more about him at school. Not only did he have a Jewish background, he was bisexual: it is thought he fell in love four times, once with a woman and three times with men.

Interested, originally, in flying and so aeronautic engineering he studied how kites fly in the upper atmosphere for his PhD in Manchester: flying the kites in the Peak District. He moved on to the study of propellors and designed a very advanced propellor that included mini jet engines on the propellor blades themselves. Studying propellors led him to an interest in advanced mathematics and then ultimately to the foundations of mathematics – a course about which, years later, he taught at Cambridge University that Alan Turing attended. Turing was teaching a course with the same title but from a completely different point of view at the time. His interest in the foundations of maths led to him thinking about what facts are, how they relate to thoughts, language and logic and what truth really was. However, World War I then broke out. During the war he fought for the Austro-Hungarian army, originally safe behind the lines but at his own request he was sent to the Russian Front. He was ultimately awarded medals for bravery. While on military leave towards the end of the war he completed the philosophical work that made him famous, the Tractatus Logico-Philosophicus. After the war though he went to rural Austria and worked as a monastery gardener and then as a primary school teacher. His sister suggested this was “like using a precision instrument to open crates”, though as he got into trouble for being violent in his punishments of the children the metaphor probably isn’t very good as he doesn’t sound like a great teacher and as a teacher he was more like a very blunt instrument.

In his absence, his fame in academia grew, however, and so eventually he returned to Cambridge, finally gained a PhD and ultimately became a fellow and then a Professor of Philosophy. By the time World War II broke out he was teaching philosophy in Cambridge but felt this was the wrong thing to be doing during a war, so despite now being a world famous philosopher went to work as a porter in Guy’s hospital, London.

His philosophical work was ground breaking mainly because of his arguments about language and meaning with respect to truth. However, a small part of has work has a very concrete relevance to computing. His thinking about truth and logic had led him to introduce the really important idea of a tautology as a redundant statement in logic. The ancient Greeks used the word but in a completely different sense of something made “true” just because it was said more than once, so argued to be true in a rhetorical sense. In computational terms Wittgenstein’s idea of a tautology is a logical statement about propositions that can be simplified to true. Propositions are just basic statements that may or may not be true, such as “The moon is made of cheese”. An example of a tautology is (a OR NOT(a)) where (a) is a variable that stands for a proposition so something that is either true or false. Putting in the concrete propositions “The moon is made of cheese” we get:

“(The moon is made of cheese) OR NOT (The moon is made of cheese)”

or in other words the statement

“The moon is made of cheese OR The moon is NOT made of cheese”

Logically, this is always true, whatever the moon is made of. “The moon is made of cheese” can be either true or false. Either it is made of cheese or not but either way the whole statement is true whatever the truth of the moon as one side or other of the OR is bound to be true. The statement is equivalent to just saying

“TRUE”

In other words, the original statement always simplifies to truth. More than that, whatever proposition you substitute in place of the statement “The moon is made of cheese” it still simplifies to true eg if we use the statement instead “Snoopy fought the Red Baron” then we get

“Snoopy fought the Red Baron OR NOT (Snoopy fought the Red Baron)”

Again, whatever the truth about Snoopy, this is a true statement. It is true whatever statement we substitute for (a) and whether it is true or false: (a OR NOT(a)) is a tautology guaranteed to be true by its logical structure, not by the meaning of the words of the propositions substituted in for a.

As part of this work Wittgenstein used truth tables, and is often claimed to have invented them. He certainly popularised them as a result of his work becoming so famous. However, Charles Sanders Peirce used truth tables first, 30 years earlier. The latter was a philosopher too, know as the “Father of Pragmatism” (so hopefully that means he wouldn’t have minded Wittgenstein getting all the credit!)

A truth table is just a table that includes as rows all the combinations of true and false values of the variables in logical expressions together with an answer for those values. For example a truth table for the operator NOT, so telling us in all situations what (NOT a) means, is:

aNOT a
TRUEFALSE
FALSETRUE
A truth table for the NOT operator. Reading along the rows,
IF a is TRUE then (NOT a) is FALSE; IF a is FALSE then (NOT a) is TRUE. Image by CS4FN

The first thing that is important about truth tables is that they give very clear and simple meaning (or “semantics”) to logical operators (like AND, OR and NOT) and so of statements asserting facts logically. Computationally, they make precise what the logical operators do, as the above table for NOT does. This of course matters a lot in programs where logical operators control what the program does. It also matters in hardware which is built up from circuits representing the logical operations. They provide the basis for understanding what both programs and hardware do.

The following is the truth table for the logical OR operator: again the last column gives the meaning of the operator so the answer of computing the logical or operation. This time there are two variables (a) and (b) so four rows to cover the combinations.

aba OR b
TRUETRUETRUE
TRUEFALSETRUE
FALSETRUETRUE
FALSEFALSEFALSE
A truth table for the logical OR operator. Reading along the rows,
IF a is TRUE and b is TRUE then (a OR b) is TRUE;
IF a is TRUE and b is FALSE then (a OR b) is TRUE;
IF a is FALSE and b is TRUE then (a OR b) is TRUE;
IF a is FALSE and b is FASLE then (a OR b) is FALSE;
Image by CS4FN

Truth tables can be used to give more than just meaning to operators, they can be used for doing logical reasoning; to compute new truth tables for more complex logical expressions, including checking if they are tautologies. This is the basis of program verification (mathematically proving a program does the right thing) and similarly hardware verification. Let us look at (a OR (NOT a)). We make a column for (a) and then a second column gives the answer for (NOT a) from the NOT truth table. Adding a third column we then look up in the OR truth table the answers given the values for (a) and (NOT a) on each row. For example, if a is TRUE then NOT a is FALSE. Looking up the row for TRUE/FALSE in the OR table we see the answer is TRUE so that goes in the answer column for (a OR (NOT a)). The full table is then:

aNOT aa OR (NOT a)
TRUEFALSETRUE
FALSETRUETRUE
A truth table for the a OR NOT a. Reading along the rows,
IF a is TRUE then (a OR (NOT a)) is TRUE;
IF a is FALSE then (a OR (NOT a)) is TRUE;
Image by CS4FN

Truth tables therefore give us an easy way to see if a logical expression is a tautology. If the answer column has TRUE as the answer for every row, as here, then the expression is a tautology. Whatever the truth of the starting fact a, the expression is always true. It has the same truth table as the expression TRUE (a) where TRUE is an operator which gives answer true whatever its operand.

aTRUE
TRUETRUE
FALSETRUE
A truth table for the TRUE operator. Whatever its operand it gives answer TRUE.
Image by CS4FN

We can do a similar thing for (a AND (NOT a)). We need the truth table for AND to do this.

aba AND b
TRUETRUETRUE
TRUEFALSEFALSE
FALSETRUEFALSE
FALSEFALSEFALSE
A truth table for the logical AND operator.
Image by CS4FN

We fill in the answer column based on the values from the (a) column and the (NOT a) column looking up the answer in the truth table for AND.

aNOT aa AND (NOT a)
TRUEFALSEFALSE
FALSETRUEFALSE
A truth table for the a AND (NOT a). Reading along the rows,
IF a is TRUE then a AND (NOT a) is FALSE;
IF a is FALSE then a AND (NOT a) is FALSE;
Image by CS4FN

This shows that it is not a tautology as not all rows have answer TRUE. In fact, we can see from the table that this actually simplifies to FALSE. It can never be true whatever the facts involved as both (a) and (NOT a) are never true about any proposition (a) at the same time.

Here is a slightly more complicated logical expression to consider: ((a AND b) IMPLIES a). Is this a tautology? We need the truth table for IMPLIES to work this out:

aba IMPLIES b
TRUETRUETRUE
TRUEFALSEFALSE
FALSETRUETRUE
FALSEFALSETRUE
A truth table for the logical IMPLIES logical operator.
Image by CS4FN

When we look up the values from the (a AND b) column and the (a) column in the IMPLIES truth table, we get the answers for the full expression ((a AND b) IMPLIES a) and find that it is a tautology as the answer is always true:

aba AND ba(a AND b) IMPLIES a
TRUETRUETRUETRUETRUE
TRUEFALSEFALSETRUETRUE
FALSETRUEFALSEFALSETRUE
FALSEFALSEFALSEFALSETRUE
A truth table for the logical expression (a AND b) IMPLIES a.
Image by CS4FN

Using the same kind of approach we can use truth tables to check if two expressions are equivalent. If they give the same final column of answers for the same inputs then they are interchangeable. Let’s look at (b OR (NOT a)).

abNOT a(b OR (NOT a))
TRUETRUEFALSETRUE
TRUEFALSEFALSEFALSE
FALSETRUETRUETRUE
FALSEFALSETRUETRUE
A Truth table for the logical expression (b OR (NOT a)).
Image by CS4FN

This gives exactly the same answers in the final column as the truth table for IMPLIES above, so we have just shown that:

(a IMPLIES b) IS EQUIVALENT TO (b OR (NOT a))

We have proved a theorem about logical implication. (a IMPLIES b) has the same meaning as, so is interchangeable with, (b OR (NOT a)). All tautologies are interchangeable of course as they are all equivalent in their answers to TRUE. If we give a truth table for IS EQUIVALENT TO we could even show equivalences like the above are tautologies!

Tautologies, and equivalences, once proved, can also be the basis of further reasoning. Any time we have in a logical expression (a IMPLES b), for example, we can swap it for (b OR (NOT a)) knowing they are equivalent.

Truth tables helped Wittgenstein think about arguments and deduction of facts using rules. In particular, he decided special rules that other philosophers suggested should be used in deduction, were not necessary, as such. Deduction instead works simply from the structure of logic that means logical statements follow from other logical statements. Truth tables gave a clear way to see the equivalences resulting from the logic. Deduction is not about meanings in language but about logic. Truth tables meant you could decide if something was true by looking at equivalences so ultimately tautologies. They showed that some statements were universally true just by inspection of the truth table. For computer scientists they gave a way to define what logical operations mean and then reason about digital circuits and programs they designed, both to help understand, so write them, and get them right.

Wittgenstein started off as an engineer interested in building flying machines, moved to become a mathematician, a soldier, a gardener and a teacher, as well as a hospital porter, but ultimately he is remembered as a great philosopher. Abstract though his philosophy was, along the way he provided computer scientists and electrical engineers useful tools that helped them build thinking machines.

– Paul Curzon, Queen Mary University of London

More on …

Related Magazines …

cs4fn Issue 14 ccover

Subscribe to be notified whenever we publish a new post to the CS4FN blog.

This page is funded by EPSRC on research agreement EP/W033615/1.

QMUL CS4FN EPSRC logos

EPSRC also supported this blog post through research grant EP/K040251/2 held by Professor Ursula Martin. 

Alan Turing’s life

by Jonathan Black, Paul Curzon and Peter W. McOwan, Queen Mary University of London

From the archive

Alan Turing Portrait
Image of Alan Turing: Elliott & Fry, Public domain, via Wikimedia Commons

Alan Turing was born in London on 23 June 1912. His parents were both from successful, well-to-do families, which in the early part of the 20th century in England meant that his childhood was pretty stuffy. He didn’t see his parents much, wasn’t encouraged to be creative, and certainly wasn’t encouraged in his interest in science. But even early in his life, science was what he loved to do. He kept up his interest while he was away at boarding school, even though his teachers thought it was beneath well-bred students. When he was 16 he met a boy called Christopher Morcom who was also very interested in science. Christopher became Alan’s best friend, and probably his first big crush. When Christopher died suddenly a couple of years later, Alan partly helped deal with his grief with science, by studying whether the mind was made of matter, and where – if anywhere – the mind went when someone died.

The Turing machine

After he finished school, Alan went to the University of Cambridge to study mathematics, which brought him closer to questions about logic and calculation (and mind). After he graduated he stayed at Cambridge as a fellow, and started working on a problem that had been giving mathematicians headaches: whether it was possible to determine in advance if a particular mathematical proposition was provable. Alan solved it (the answer was no), but it was the way he solved it that helped change the world. He imagined a machine that could move symbols around on a paper tape to calculate answers. It would be like a mind, said Alan, only mechanical. You could give it a set of instructions to follow, the machine would move the symbols around and you would have your answer. This imaginary machine came to be called a Turing machine, and it forms the basis of how modern computers work.

Code-breaking at Bletchley Park

By the time the Second World War came round, Alan was a successful mathematician who’d spent time working with the greatest minds in his field. The British government needed mathematicians to help them crack the German codes so they could read their secret communiqués. Alan had been helping them on and off already, but when war broke out he moved to the British code-breaking headquarters at Bletchley Park to work full-time. Based on work by Polish mathematicians, he helped crack one of the Germans’ most baffling codes, called the Enigma, by designing a machine (based on earlier version by the Poles again!) that could help break Enigma messages as long as you could guess a small bit of the text (see box). With the help of British intelligence that guesswork was possible, so Alan and his team began regularly deciphering messages from ships and U-boats. As the war went on the codes got harder, but Alan and his colleagues at Bletchley designed even more impressive machines. They brought in telephone engineers to help marry Alan’s ideas about logic and statistics with electronic circuitry. That combination was about to produce the modern world.

Building a brain

The problem was that the engineers and code-breakers were still having to make a new machine for every job they wanted it to do. But Alan still had his idea for the Turing machine, which could do any calculation as long as you gave it different instructions. By the end of the war Alan was ready to have a go at building a Turing machine in real life. If it all went to plan, it would be the first modern electronic computer, but Alan thought of it as “building a brain”. Others were interested in building a brain, though, and soon there were teams elsewhere in the UK and the USA in the race too. Eventually a group in Manchester made Alan’s ideas a reality.

Troubled times

Not long after, he went to work at Manchester himself. He started thinking about new and different questions, like whether machines could be intelligent, and how plants and animals get their shape. But before he had much of a chance to explore these interests, Alan was arrested. In the 1950s, gay sex was illegal in the UK, and the police had discovered Alan’s relationship with a man. Alan didn’t hide his sexuality from his friends, and at his trial Alan never denied that he had relationships with men. He simply said that he didn’t see what was wrong with it. He was convicted, and forced to take hormone injections for a year as a form of chemical castration.

Although he had had a very rough period in his life, he kept living as well as possible, becoming closer to his friends, going on holiday and continuing his work in biology and physics. Then, in June 1954, his cleaner found him dead in his bed, with a half-eaten, cyanide-laced apple beside him.

Alan’s suicide was a tragic, unjust end to a life that made so much of the future possible.

More on …

Related Magazines …

cs4fn issue 14 cover

This blog is funded through EPSRC grant EP/W033615/1.