Can you solve these two puzzles? Which is easiest?
Puzzle 1: The Tour Guide
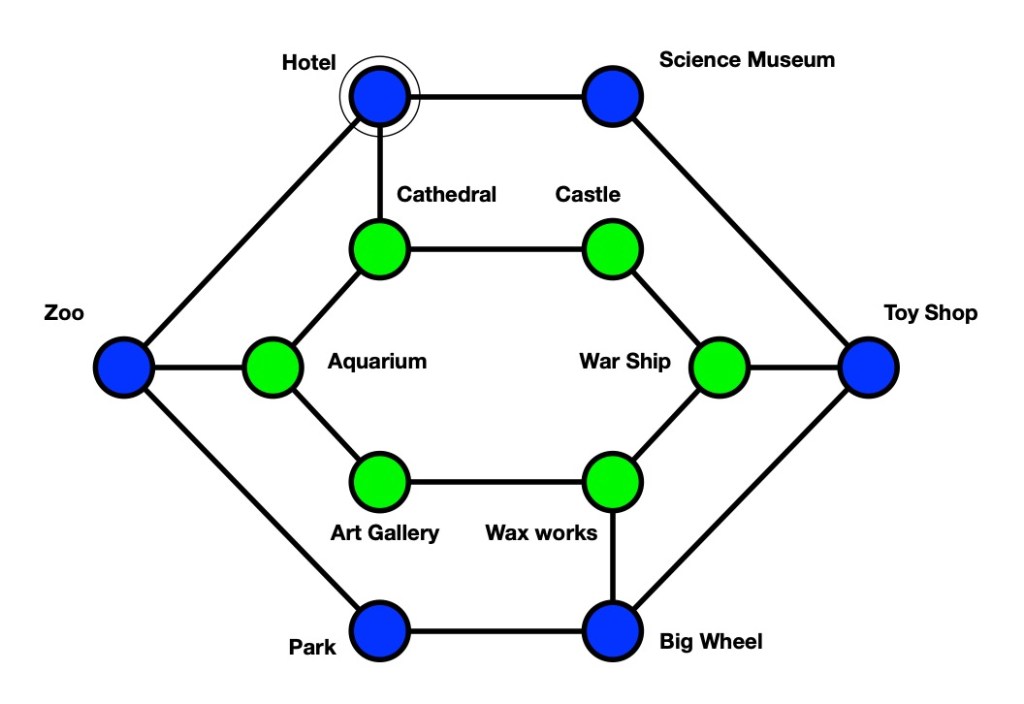
You are a tour guide. Using this travel map, find a route that starts from the hotel and visits every tourist site only once, ending back at the hotel.
Computer scientists call maps like this one a graph. A graph has circles (nodes) linked by lines (edges). This graph represents the routes between tourist attractions.
If you write down the route as a series of steps, then you have written an algorithm to do the tour.
Puzzle 2: The Knights Tour
A knight moves in Chess in an L-shape landing on a new square. For example, a knight on square 1 of the board below can move to square 6, 7 or 9.
Start with a knight (or counter) on square 1. Making only “knight” moves, visit every square exactly once, ending back at square 1.
Try and solve both puzzles before you read on. Solutions below!
https://cs4fndownloads.wordpress.com/puzzling-tours/ You can find more about these puzzles (and graphs) in our free booklet Puzzling Tours.
Solutions
Which of the two puzzles is easiest? In fact they are the same puzzle so should be just as easy as each other to solve. Most people find the Tour Guide puzzle far easier though. Why? Because the way that the relevant information is stored makes it easier to work with – here as a graph data structure.
A graph data structure is just a data structure made of nodes (points) and edges (lines connecting them). The Tour Guide puzzle is represented as a graph so is fairly easy to solve.
The Knights Tour Puzzle is not represented as a graph, but it could be. Make each square on the board a node. Then make each legal move between squares an edge connecting those nodes. You may end up with a bit of a mess of crossing lines. but tidy it up so that edges do not cross and you get the exact same graph as the Tour Guide puzzle. As we said they are the same puzzle!
Here is one solution to both the Tour Guide Puzzle and the Knights Tour Puzzle (there are several).

Subscribe to be notified whenever we publish a new post to the CS4FN blog.
This blog is funded by EPSRC on research agreement EP/W033615/1.